Using python and the pyomo library for optimization
Creating an optimized lineup for DFS NFL football
- Daily Fantasy Sports games are considered a skill-based game where participants can choose players in a sports league and earn points based on cerntain statistics. There is an entry fee for each line up submitted and the lineup with the most points wins the prize pool.
- The National Football League is the most popular of the fantasy sports.
- There are many different contests users can enter and select players such as single games, entire weekly games, and certain periods such as morning or afternoon slate of games.
- The National Football League consists of a 18 week schedule starting with Thursday Night Football and ending on Monday Night Football.
- FanDuel and DraftKings are the largest and most used daily fantasy sports sites.
- The positions needed are 1 quarterback, 2 running backs, 3 wide receivers, 1 tight end, 1 team defense and 1 flex position which can be either a running back, wide receiver or tight end.
- The data for this project was collected from rotowire.com
#Copy-and-paste the code below to use as "set-up" when your optimization model uses Pyomo and Coin-OR solvers.
#for reference, see https://jckantor.github.io/ND-Pyomo-Cookbook/notebooks/01.02-Running-Pyomo-on-Google-Colab.html#installing-pyomo-and-solvers
%%capture
import sys
import os
if 'google.colab' in sys.modules:
!pip install idaes-pse --pre
!idaes get-extensions --to ./bin
os.environ['PATH'] += ':bin'
from pyomo.environ import *
import pandas as pd
# Importing data
df = pd.read_csv('rotowire-NFL-players.csv')
df.head()
| PLAYER | POS | TEAM | OPP | ML | O/U | SPRD | TM/P | SAL | FPTS | VAL | RST% | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Kyren Williams | RB | LAR | WAS | -300 | 50.5 | -6.5 | 28.5 | 7500 | 18.65 | 2.5 | 24.92 |
| 1 | Ezekiel Elliott | RB | NE | KC | 332 | 37.5 | 8.5 | 14.5 | 5800 | 15.19 | 2.6 | 24.17 |
| 2 | Christian McCaffrey | RB | SF | ARI | -780 | 48.5 | -12.5 | 30.5 | 9300 | 23.02 | 2.5 | 23.33 |
| 3 | Antonio Gibson | RB | WAS | LAR | 241 | 50.5 | 6.5 | 22.0 | 5200 | 14.64 | 2.8 | 20.82 |
| 4 | Matthew Stafford | QB | LAR | WAS | -300 | 50.5 | -6.5 | 28.5 | 6000 | 17.19 | 2.9 | 15.14 |
Going through each column of the dataset
- Player - NFL player’s name
- POS - The skilled position which include {QB: quaterback, RB: running back, WR: wide receiver, TE: tight end, D: team defense}
- TEAM - team the position player plays for
- OPP - the opposing team for that week
- ML - the moneyline odds of the team winning. Minus odds are favorite while plus odds are underdog
- O/U - the betting total of the game that week
- SPRD - the point spread of that game. Minus points are favorite while plus points are underdog
- TM/P - points per game for that team
- SAL - the Daily Fantasy Sports salary for choosing that player
- FPTS - the fantasy points predicted
- VAL - FPTS divided by the SAL times 1000
- RST% - the percent of daily fantasy teams that the player is rostered on
df['POS'].value_counts()
WR 144
RB 91
TE 83
QB 54
D 20
Name: POS, dtype: int64
# keeping the position names
pos_names = df['POS']
df = pd.get_dummies(df, columns=['POS'])
For selecting each positioin, I have created dummy variables for each position: QB, RB, WR, TE and team defense so I can use the dummies as contraint values.
df = pd.concat([df, pos_names], axis=1)
df.head()
| PLAYER | TEAM | OPP | ML | O/U | SPRD | TM/P | SAL | FPTS | VAL | RST% | POS_D | POS_QB | POS_RB | POS_TE | POS_WR | POS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Kyren Williams | LAR | WAS | -300 | 50.5 | -6.5 | 28.5 | 7500 | 18.65 | 2.5 | 24.92 | 0 | 0 | 1 | 0 | 0 | RB |
| 1 | Ezekiel Elliott | NE | KC | 332 | 37.5 | 8.5 | 14.5 | 5800 | 15.19 | 2.6 | 24.17 | 0 | 0 | 1 | 0 | 0 | RB |
| 2 | Christian McCaffrey | SF | ARI | -780 | 48.5 | -12.5 | 30.5 | 9300 | 23.02 | 2.5 | 23.33 | 0 | 0 | 1 | 0 | 0 | RB |
| 3 | Antonio Gibson | WAS | LAR | 241 | 50.5 | 6.5 | 22.0 | 5200 | 14.64 | 2.8 | 20.82 | 0 | 0 | 1 | 0 | 0 | RB |
| 4 | Matthew Stafford | LAR | WAS | -300 | 50.5 | -6.5 | 28.5 | 6000 | 17.19 | 2.9 | 15.14 | 0 | 1 | 0 | 0 | 0 | QB |
I have created lists for salary, projected fantasy points, position and roster percentage.
#salary list
salary = df['SAL'].tolist()
#Projected Fantasy points list
projected_points = df['FPTS'].tolist()
# List for each position
QB_list = df['POS_QB'].tolist()
RB_list = df['POS_RB'].tolist()
WR_list = df['POS_WR'].tolist()
TE_list = df['POS_TE'].tolist()
DEF_list = df['POS_D'].tolist()
# Roster percent list
roster_percent = df['RST%'].tolist()
# Histogram of the roster percent. High roster percent means players are in many lineups
df.hist(column='RST%')
array([[<Axes: title={'center': 'RST%'}>]], dtype=object)
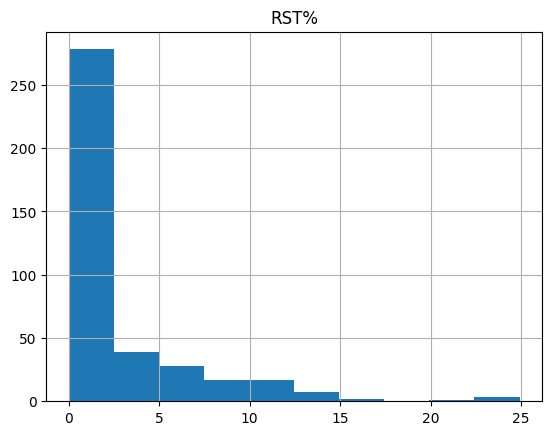
Looking at the roster percentage, we can see that the majority of players are at 0 percent. We can create a constraint where we can have the average roster percentage be over or under a certain value using roster_low as the average of the roster percent as a whole percent.
Optimization Process
- Objective: maximize the projected fantasy points
- Decision Variables: selecting the players in the data set (binary)
- Constraints:
- Select the correct number of positions: 1 quarterback, 2 running backs, 3 wide receivers, 1 tight end, 1 team defense and 1 flex
- Budget: the entire lineup needs to have a total salary or cost of $50,000 or under. The budget can be adjusted based on the Daily Fantasy Sports site as well as the number of positions.
- Rostership: we can select players that are popular or unpopular depending on the risk factor of the lineup
# Total Budget for the entire lineup
budget = 50000
# Number of positions
num_QB = 1
num_RB = 2
max_RB = 3
num_WR = 3
max_WR = 4
num_TE = 1
max_TE = 2
num_Flex = 1
num_DEF = 1
#Average of the roster percent as an whole percent
roster_low = 6
#Position Requirements
position_list = ['QB', 'RB', 'RB', 'WR', 'WR', 'WR', 'TE', 'FLEX', 'DST']
num_positions = len(position_list) #QB, RB, RB, WR, WR, WR, TE, FLEX, DEF
# Length of entire data set
n = len(salary)
#define the concrete model
model = ConcreteModel()
#DVs
model.x = Var(range(n), domain = Binary)
#objective
model.Objective = Objective(expr = sum(model.x[i]*projected_points[i] for i in range(n)), sense = maximize)
#budget constraint
model.BudgetConstraint = Constraint(expr = sum(model.x[i]*salary[i] for i in range(n)) <= budget)
# Position Constraints. We need
model.num_positionConstraint = Constraint(expr = sum(model.x[i] for i in range(n)) == num_positions)
model.QBConstraint = Constraint(expr = sum(model.x[i]*QB_list[i] for i in range(n)) == num_QB)
model.RBConstraint = Constraint(expr = sum(model.x[i]*RB_list[i] for i in range(n)) == num_RB)
model.RBConstraint = Constraint(expr = sum(model.x[i]*RB_list[i] for i in range(n)) <= max_RB)
model.WRConstraint = Constraint(expr = sum(model.x[i]*WR_list[i] for i in range(n)) == num_WR)
model.WRConstraint = Constraint(expr = sum(model.x[i]*WR_list[i] for i in range(n)) <= max_WR)
model.TEConstraint = Constraint(expr = sum(model.x[i]*TE_list[i] for i in range(n)) == num_TE)
model.TEConstraint = Constraint(expr = sum(model.x[i]*TE_list[i] for i in range(n)) <= max_TE)
model.DEFConstraint = Constraint(expr = sum(model.x[i]*DEF_list[i] for i in range(n)) == num_DEF)
#Constraint for average roster percentage of the players chosen. We can adjust for popular or unpopular players
model.RSTConstraint = Constraint(expr = sum(model.x[i]*roster_percent[i] for i in range(n)) / num_positions >= roster_low)
# Printing the model and seeing what rows are selected
model.pprint()
WARNING:pyomo.core:Implicitly replacing the Component attribute RBConstraint (type=<class 'pyomo.core.base.constraint.ScalarConstraint'>) on block unknown with a new Component (type=<class 'pyomo.core.base.constraint.AbstractScalarConstraint'>).
This is usually indicative of a modelling error.
To avoid this warning, use block.del_component() and block.add_component().
WARNING:pyomo.core:Implicitly replacing the Component attribute WRConstraint (type=<class 'pyomo.core.base.constraint.ScalarConstraint'>) on block unknown with a new Component (type=<class 'pyomo.core.base.constraint.AbstractScalarConstraint'>).
This is usually indicative of a modelling error.
To avoid this warning, use block.del_component() and block.add_component().
WARNING:pyomo.core:Implicitly replacing the Component attribute TEConstraint (type=<class 'pyomo.core.base.constraint.ScalarConstraint'>) on block unknown with a new Component (type=<class 'pyomo.core.base.constraint.AbstractScalarConstraint'>).
This is usually indicative of a modelling error.
To avoid this warning, use block.del_component() and block.add_component().
1 Var Declarations
x : Size=392, Index={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314, 315, 316, 317, 318, 319, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329, 330, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 343, 344, 345, 346, 347, 348, 349, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359, 360, 361, 362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377, 378, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391}
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : 0 : None : 1 : False : True : Binary
1 : 0 : None : 1 : False : True : Binary
2 : 0 : None : 1 : False : True : Binary
3 : 0 : None : 1 : False : True : Binary
4 : 0 : None : 1 : False : True : Binary
5 : 0 : None : 1 : False : True : Binary
6 : 0 : None : 1 : False : True : Binary
7 : 0 : None : 1 : False : True : Binary
8 : 0 : None : 1 : False : True : Binary
9 : 0 : None : 1 : False : True : Binary
10 : 0 : None : 1 : False : True : Binary
11 : 0 : None : 1 : False : True : Binary
12 : 0 : None : 1 : False : True : Binary
13 : 0 : None : 1 : False : True : Binary
14 : 0 : None : 1 : False : True : Binary
15 : 0 : None : 1 : False : True : Binary
16 : 0 : None : 1 : False : True : Binary
17 : 0 : None : 1 : False : True : Binary
18 : 0 : None : 1 : False : True : Binary
19 : 0 : None : 1 : False : True : Binary
20 : 0 : None : 1 : False : True : Binary
21 : 0 : None : 1 : False : True : Binary
22 : 0 : None : 1 : False : True : Binary
23 : 0 : None : 1 : False : True : Binary
24 : 0 : None : 1 : False : True : Binary
25 : 0 : None : 1 : False : True : Binary
26 : 0 : None : 1 : False : True : Binary
27 : 0 : None : 1 : False : True : Binary
28 : 0 : None : 1 : False : True : Binary
29 : 0 : None : 1 : False : True : Binary
30 : 0 : None : 1 : False : True : Binary
31 : 0 : None : 1 : False : True : Binary
32 : 0 : None : 1 : False : True : Binary
33 : 0 : None : 1 : False : True : Binary
34 : 0 : None : 1 : False : True : Binary
35 : 0 : None : 1 : False : True : Binary
36 : 0 : None : 1 : False : True : Binary
37 : 0 : None : 1 : False : True : Binary
38 : 0 : None : 1 : False : True : Binary
39 : 0 : None : 1 : False : True : Binary
40 : 0 : None : 1 : False : True : Binary
41 : 0 : None : 1 : False : True : Binary
42 : 0 : None : 1 : False : True : Binary
43 : 0 : None : 1 : False : True : Binary
44 : 0 : None : 1 : False : True : Binary
45 : 0 : None : 1 : False : True : Binary
46 : 0 : None : 1 : False : True : Binary
47 : 0 : None : 1 : False : True : Binary
48 : 0 : None : 1 : False : True : Binary
49 : 0 : None : 1 : False : True : Binary
50 : 0 : None : 1 : False : True : Binary
51 : 0 : None : 1 : False : True : Binary
52 : 0 : None : 1 : False : True : Binary
53 : 0 : None : 1 : False : True : Binary
54 : 0 : None : 1 : False : True : Binary
55 : 0 : None : 1 : False : True : Binary
56 : 0 : None : 1 : False : True : Binary
57 : 0 : None : 1 : False : True : Binary
58 : 0 : None : 1 : False : True : Binary
59 : 0 : None : 1 : False : True : Binary
60 : 0 : None : 1 : False : True : Binary
61 : 0 : None : 1 : False : True : Binary
62 : 0 : None : 1 : False : True : Binary
63 : 0 : None : 1 : False : True : Binary
64 : 0 : None : 1 : False : True : Binary
65 : 0 : None : 1 : False : True : Binary
66 : 0 : None : 1 : False : True : Binary
67 : 0 : None : 1 : False : True : Binary
68 : 0 : None : 1 : False : True : Binary
69 : 0 : None : 1 : False : True : Binary
70 : 0 : None : 1 : False : True : Binary
71 : 0 : None : 1 : False : True : Binary
72 : 0 : None : 1 : False : True : Binary
73 : 0 : None : 1 : False : True : Binary
74 : 0 : None : 1 : False : True : Binary
75 : 0 : None : 1 : False : True : Binary
76 : 0 : None : 1 : False : True : Binary
77 : 0 : None : 1 : False : True : Binary
78 : 0 : None : 1 : False : True : Binary
79 : 0 : None : 1 : False : True : Binary
80 : 0 : None : 1 : False : True : Binary
81 : 0 : None : 1 : False : True : Binary
82 : 0 : None : 1 : False : True : Binary
83 : 0 : None : 1 : False : True : Binary
84 : 0 : None : 1 : False : True : Binary
85 : 0 : None : 1 : False : True : Binary
86 : 0 : None : 1 : False : True : Binary
87 : 0 : None : 1 : False : True : Binary
88 : 0 : None : 1 : False : True : Binary
89 : 0 : None : 1 : False : True : Binary
90 : 0 : None : 1 : False : True : Binary
91 : 0 : None : 1 : False : True : Binary
92 : 0 : None : 1 : False : True : Binary
93 : 0 : None : 1 : False : True : Binary
94 : 0 : None : 1 : False : True : Binary
95 : 0 : None : 1 : False : True : Binary
96 : 0 : None : 1 : False : True : Binary
97 : 0 : None : 1 : False : True : Binary
98 : 0 : None : 1 : False : True : Binary
99 : 0 : None : 1 : False : True : Binary
100 : 0 : None : 1 : False : True : Binary
101 : 0 : None : 1 : False : True : Binary
102 : 0 : None : 1 : False : True : Binary
103 : 0 : None : 1 : False : True : Binary
104 : 0 : None : 1 : False : True : Binary
105 : 0 : None : 1 : False : True : Binary
106 : 0 : None : 1 : False : True : Binary
107 : 0 : None : 1 : False : True : Binary
108 : 0 : None : 1 : False : True : Binary
109 : 0 : None : 1 : False : True : Binary
110 : 0 : None : 1 : False : True : Binary
111 : 0 : None : 1 : False : True : Binary
112 : 0 : None : 1 : False : True : Binary
113 : 0 : None : 1 : False : True : Binary
114 : 0 : None : 1 : False : True : Binary
115 : 0 : None : 1 : False : True : Binary
116 : 0 : None : 1 : False : True : Binary
117 : 0 : None : 1 : False : True : Binary
118 : 0 : None : 1 : False : True : Binary
119 : 0 : None : 1 : False : True : Binary
120 : 0 : None : 1 : False : True : Binary
121 : 0 : None : 1 : False : True : Binary
122 : 0 : None : 1 : False : True : Binary
123 : 0 : None : 1 : False : True : Binary
124 : 0 : None : 1 : False : True : Binary
125 : 0 : None : 1 : False : True : Binary
126 : 0 : None : 1 : False : True : Binary
127 : 0 : None : 1 : False : True : Binary
128 : 0 : None : 1 : False : True : Binary
129 : 0 : None : 1 : False : True : Binary
130 : 0 : None : 1 : False : True : Binary
131 : 0 : None : 1 : False : True : Binary
132 : 0 : None : 1 : False : True : Binary
133 : 0 : None : 1 : False : True : Binary
134 : 0 : None : 1 : False : True : Binary
135 : 0 : None : 1 : False : True : Binary
136 : 0 : None : 1 : False : True : Binary
137 : 0 : None : 1 : False : True : Binary
138 : 0 : None : 1 : False : True : Binary
139 : 0 : None : 1 : False : True : Binary
140 : 0 : None : 1 : False : True : Binary
141 : 0 : None : 1 : False : True : Binary
142 : 0 : None : 1 : False : True : Binary
143 : 0 : None : 1 : False : True : Binary
144 : 0 : None : 1 : False : True : Binary
145 : 0 : None : 1 : False : True : Binary
146 : 0 : None : 1 : False : True : Binary
147 : 0 : None : 1 : False : True : Binary
148 : 0 : None : 1 : False : True : Binary
149 : 0 : None : 1 : False : True : Binary
150 : 0 : None : 1 : False : True : Binary
151 : 0 : None : 1 : False : True : Binary
152 : 0 : None : 1 : False : True : Binary
153 : 0 : None : 1 : False : True : Binary
154 : 0 : None : 1 : False : True : Binary
155 : 0 : None : 1 : False : True : Binary
156 : 0 : None : 1 : False : True : Binary
157 : 0 : None : 1 : False : True : Binary
158 : 0 : None : 1 : False : True : Binary
159 : 0 : None : 1 : False : True : Binary
160 : 0 : None : 1 : False : True : Binary
161 : 0 : None : 1 : False : True : Binary
162 : 0 : None : 1 : False : True : Binary
163 : 0 : None : 1 : False : True : Binary
164 : 0 : None : 1 : False : True : Binary
165 : 0 : None : 1 : False : True : Binary
166 : 0 : None : 1 : False : True : Binary
167 : 0 : None : 1 : False : True : Binary
168 : 0 : None : 1 : False : True : Binary
169 : 0 : None : 1 : False : True : Binary
170 : 0 : None : 1 : False : True : Binary
171 : 0 : None : 1 : False : True : Binary
172 : 0 : None : 1 : False : True : Binary
173 : 0 : None : 1 : False : True : Binary
174 : 0 : None : 1 : False : True : Binary
175 : 0 : None : 1 : False : True : Binary
176 : 0 : None : 1 : False : True : Binary
177 : 0 : None : 1 : False : True : Binary
178 : 0 : None : 1 : False : True : Binary
179 : 0 : None : 1 : False : True : Binary
180 : 0 : None : 1 : False : True : Binary
181 : 0 : None : 1 : False : True : Binary
182 : 0 : None : 1 : False : True : Binary
183 : 0 : None : 1 : False : True : Binary
184 : 0 : None : 1 : False : True : Binary
185 : 0 : None : 1 : False : True : Binary
186 : 0 : None : 1 : False : True : Binary
187 : 0 : None : 1 : False : True : Binary
188 : 0 : None : 1 : False : True : Binary
189 : 0 : None : 1 : False : True : Binary
190 : 0 : None : 1 : False : True : Binary
191 : 0 : None : 1 : False : True : Binary
192 : 0 : None : 1 : False : True : Binary
193 : 0 : None : 1 : False : True : Binary
194 : 0 : None : 1 : False : True : Binary
195 : 0 : None : 1 : False : True : Binary
196 : 0 : None : 1 : False : True : Binary
197 : 0 : None : 1 : False : True : Binary
198 : 0 : None : 1 : False : True : Binary
199 : 0 : None : 1 : False : True : Binary
200 : 0 : None : 1 : False : True : Binary
201 : 0 : None : 1 : False : True : Binary
202 : 0 : None : 1 : False : True : Binary
203 : 0 : None : 1 : False : True : Binary
204 : 0 : None : 1 : False : True : Binary
205 : 0 : None : 1 : False : True : Binary
206 : 0 : None : 1 : False : True : Binary
207 : 0 : None : 1 : False : True : Binary
208 : 0 : None : 1 : False : True : Binary
209 : 0 : None : 1 : False : True : Binary
210 : 0 : None : 1 : False : True : Binary
211 : 0 : None : 1 : False : True : Binary
212 : 0 : None : 1 : False : True : Binary
213 : 0 : None : 1 : False : True : Binary
214 : 0 : None : 1 : False : True : Binary
215 : 0 : None : 1 : False : True : Binary
216 : 0 : None : 1 : False : True : Binary
217 : 0 : None : 1 : False : True : Binary
218 : 0 : None : 1 : False : True : Binary
219 : 0 : None : 1 : False : True : Binary
220 : 0 : None : 1 : False : True : Binary
221 : 0 : None : 1 : False : True : Binary
222 : 0 : None : 1 : False : True : Binary
223 : 0 : None : 1 : False : True : Binary
224 : 0 : None : 1 : False : True : Binary
225 : 0 : None : 1 : False : True : Binary
226 : 0 : None : 1 : False : True : Binary
227 : 0 : None : 1 : False : True : Binary
228 : 0 : None : 1 : False : True : Binary
229 : 0 : None : 1 : False : True : Binary
230 : 0 : None : 1 : False : True : Binary
231 : 0 : None : 1 : False : True : Binary
232 : 0 : None : 1 : False : True : Binary
233 : 0 : None : 1 : False : True : Binary
234 : 0 : None : 1 : False : True : Binary
235 : 0 : None : 1 : False : True : Binary
236 : 0 : None : 1 : False : True : Binary
237 : 0 : None : 1 : False : True : Binary
238 : 0 : None : 1 : False : True : Binary
239 : 0 : None : 1 : False : True : Binary
240 : 0 : None : 1 : False : True : Binary
241 : 0 : None : 1 : False : True : Binary
242 : 0 : None : 1 : False : True : Binary
243 : 0 : None : 1 : False : True : Binary
244 : 0 : None : 1 : False : True : Binary
245 : 0 : None : 1 : False : True : Binary
246 : 0 : None : 1 : False : True : Binary
247 : 0 : None : 1 : False : True : Binary
248 : 0 : None : 1 : False : True : Binary
249 : 0 : None : 1 : False : True : Binary
250 : 0 : None : 1 : False : True : Binary
251 : 0 : None : 1 : False : True : Binary
252 : 0 : None : 1 : False : True : Binary
253 : 0 : None : 1 : False : True : Binary
254 : 0 : None : 1 : False : True : Binary
255 : 0 : None : 1 : False : True : Binary
256 : 0 : None : 1 : False : True : Binary
257 : 0 : None : 1 : False : True : Binary
258 : 0 : None : 1 : False : True : Binary
259 : 0 : None : 1 : False : True : Binary
260 : 0 : None : 1 : False : True : Binary
261 : 0 : None : 1 : False : True : Binary
262 : 0 : None : 1 : False : True : Binary
263 : 0 : None : 1 : False : True : Binary
264 : 0 : None : 1 : False : True : Binary
265 : 0 : None : 1 : False : True : Binary
266 : 0 : None : 1 : False : True : Binary
267 : 0 : None : 1 : False : True : Binary
268 : 0 : None : 1 : False : True : Binary
269 : 0 : None : 1 : False : True : Binary
270 : 0 : None : 1 : False : True : Binary
271 : 0 : None : 1 : False : True : Binary
272 : 0 : None : 1 : False : True : Binary
273 : 0 : None : 1 : False : True : Binary
274 : 0 : None : 1 : False : True : Binary
275 : 0 : None : 1 : False : True : Binary
276 : 0 : None : 1 : False : True : Binary
277 : 0 : None : 1 : False : True : Binary
278 : 0 : None : 1 : False : True : Binary
279 : 0 : None : 1 : False : True : Binary
280 : 0 : None : 1 : False : True : Binary
281 : 0 : None : 1 : False : True : Binary
282 : 0 : None : 1 : False : True : Binary
283 : 0 : None : 1 : False : True : Binary
284 : 0 : None : 1 : False : True : Binary
285 : 0 : None : 1 : False : True : Binary
286 : 0 : None : 1 : False : True : Binary
287 : 0 : None : 1 : False : True : Binary
288 : 0 : None : 1 : False : True : Binary
289 : 0 : None : 1 : False : True : Binary
290 : 0 : None : 1 : False : True : Binary
291 : 0 : None : 1 : False : True : Binary
292 : 0 : None : 1 : False : True : Binary
293 : 0 : None : 1 : False : True : Binary
294 : 0 : None : 1 : False : True : Binary
295 : 0 : None : 1 : False : True : Binary
296 : 0 : None : 1 : False : True : Binary
297 : 0 : None : 1 : False : True : Binary
298 : 0 : None : 1 : False : True : Binary
299 : 0 : None : 1 : False : True : Binary
300 : 0 : None : 1 : False : True : Binary
301 : 0 : None : 1 : False : True : Binary
302 : 0 : None : 1 : False : True : Binary
303 : 0 : None : 1 : False : True : Binary
304 : 0 : None : 1 : False : True : Binary
305 : 0 : None : 1 : False : True : Binary
306 : 0 : None : 1 : False : True : Binary
307 : 0 : None : 1 : False : True : Binary
308 : 0 : None : 1 : False : True : Binary
309 : 0 : None : 1 : False : True : Binary
310 : 0 : None : 1 : False : True : Binary
311 : 0 : None : 1 : False : True : Binary
312 : 0 : None : 1 : False : True : Binary
313 : 0 : None : 1 : False : True : Binary
314 : 0 : None : 1 : False : True : Binary
315 : 0 : None : 1 : False : True : Binary
316 : 0 : None : 1 : False : True : Binary
317 : 0 : None : 1 : False : True : Binary
318 : 0 : None : 1 : False : True : Binary
319 : 0 : None : 1 : False : True : Binary
320 : 0 : None : 1 : False : True : Binary
321 : 0 : None : 1 : False : True : Binary
322 : 0 : None : 1 : False : True : Binary
323 : 0 : None : 1 : False : True : Binary
324 : 0 : None : 1 : False : True : Binary
325 : 0 : None : 1 : False : True : Binary
326 : 0 : None : 1 : False : True : Binary
327 : 0 : None : 1 : False : True : Binary
328 : 0 : None : 1 : False : True : Binary
329 : 0 : None : 1 : False : True : Binary
330 : 0 : None : 1 : False : True : Binary
331 : 0 : None : 1 : False : True : Binary
332 : 0 : None : 1 : False : True : Binary
333 : 0 : None : 1 : False : True : Binary
334 : 0 : None : 1 : False : True : Binary
335 : 0 : None : 1 : False : True : Binary
336 : 0 : None : 1 : False : True : Binary
337 : 0 : None : 1 : False : True : Binary
338 : 0 : None : 1 : False : True : Binary
339 : 0 : None : 1 : False : True : Binary
340 : 0 : None : 1 : False : True : Binary
341 : 0 : None : 1 : False : True : Binary
342 : 0 : None : 1 : False : True : Binary
343 : 0 : None : 1 : False : True : Binary
344 : 0 : None : 1 : False : True : Binary
345 : 0 : None : 1 : False : True : Binary
346 : 0 : None : 1 : False : True : Binary
347 : 0 : None : 1 : False : True : Binary
348 : 0 : None : 1 : False : True : Binary
349 : 0 : None : 1 : False : True : Binary
350 : 0 : None : 1 : False : True : Binary
351 : 0 : None : 1 : False : True : Binary
352 : 0 : None : 1 : False : True : Binary
353 : 0 : None : 1 : False : True : Binary
354 : 0 : None : 1 : False : True : Binary
355 : 0 : None : 1 : False : True : Binary
356 : 0 : None : 1 : False : True : Binary
357 : 0 : None : 1 : False : True : Binary
358 : 0 : None : 1 : False : True : Binary
359 : 0 : None : 1 : False : True : Binary
360 : 0 : None : 1 : False : True : Binary
361 : 0 : None : 1 : False : True : Binary
362 : 0 : None : 1 : False : True : Binary
363 : 0 : None : 1 : False : True : Binary
364 : 0 : None : 1 : False : True : Binary
365 : 0 : None : 1 : False : True : Binary
366 : 0 : None : 1 : False : True : Binary
367 : 0 : None : 1 : False : True : Binary
368 : 0 : None : 1 : False : True : Binary
369 : 0 : None : 1 : False : True : Binary
370 : 0 : None : 1 : False : True : Binary
371 : 0 : None : 1 : False : True : Binary
372 : 0 : None : 1 : False : True : Binary
373 : 0 : None : 1 : False : True : Binary
374 : 0 : None : 1 : False : True : Binary
375 : 0 : None : 1 : False : True : Binary
376 : 0 : None : 1 : False : True : Binary
377 : 0 : None : 1 : False : True : Binary
378 : 0 : None : 1 : False : True : Binary
379 : 0 : None : 1 : False : True : Binary
380 : 0 : None : 1 : False : True : Binary
381 : 0 : None : 1 : False : True : Binary
382 : 0 : None : 1 : False : True : Binary
383 : 0 : None : 1 : False : True : Binary
384 : 0 : None : 1 : False : True : Binary
385 : 0 : None : 1 : False : True : Binary
386 : 0 : None : 1 : False : True : Binary
387 : 0 : None : 1 : False : True : Binary
388 : 0 : None : 1 : False : True : Binary
389 : 0 : None : 1 : False : True : Binary
390 : 0 : None : 1 : False : True : Binary
391 : 0 : None : 1 : False : True : Binary
1 Objective Declarations
Objective : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : maximize : 18.65*x[0] + 15.19*x[1] + 23.02*x[2] + 14.64*x[3] + 17.19*x[4] + 14.15*x[5] + 14.06*x[6] + 7.58*x[7] + 13.36*x[8] + 6.89*x[9] + 11.8*x[10] + 9.32*x[11] + 14.69*x[12] + 6.94*x[13] + 14.8*x[14] + 13.81*x[15] + 14.6*x[16] + 17.41*x[17] + 8.68*x[18] + 15.26*x[19] + 14.36*x[20] + 23.46*x[21] + 15.51*x[22] + 14.65*x[23] + 10.83*x[24] + 5.57*x[25] + 15.06*x[26] + 13.21*x[27] + 13.32*x[28] + 13.82*x[29] + 8.06*x[30] + 15.31*x[31] + 11.64*x[32] + 17.98*x[33] + 5.43*x[34] + 11.59*x[35] + 8.72*x[36] + 8.2*x[37] + 17.09*x[38] + 13.85*x[39] + 13.87*x[40] + 7.74*x[41] + 10.0*x[42] + 13.41*x[43] + 18.39*x[44] + 11.85*x[45] + 7.2*x[46] + 14.9*x[47] + 5.75*x[48] + 8.78*x[49] + 11.31*x[50] + 12.71*x[51] + 10.84*x[52] + 13.64*x[53] + 12.02*x[54] + 9.15*x[55] + 8.79*x[56] + 17.45*x[57] + 18.58*x[58] + 7.42*x[59] + 10.14*x[60] + 19.17*x[61] + 16.62*x[62] + 8.23*x[63] + 10.69*x[64] + 5.39*x[65] + 9.92*x[66] + 9.18*x[67] + 8.1*x[68] + 7.15*x[69] + 19.04*x[70] + 9.33*x[71] + 9.59*x[72] + 7.06*x[73] + 6.22*x[74] + 6.87*x[75] + 17.06*x[76] + 10.69*x[77] + 7.82*x[78] + 6.48*x[79] + 10.39*x[80] + 10.22*x[81] + 5.24*x[82] + 8.41*x[83] + 7.83*x[84] + 9.23*x[85] + 5.84*x[86] + 6.34*x[87] + 9.58*x[88] + 15.06*x[89] + 8.46*x[90] + 13.93*x[91] + 13.08*x[92] + 11.39*x[93] + 6.75*x[94] + 14.48*x[95] + 13.75*x[96] + 13.85*x[97] + 9.26*x[98] + 12.92*x[99] + 6.85*x[100] + 5.42*x[101] + 4.87*x[102] + 8.35*x[103] + 16.71*x[104] + 4.87*x[105] + 6.02*x[106] + 5.71*x[107] + 8.93*x[108] + 12.66*x[109] + 10.73*x[110] + 5.61*x[111] + 7.98*x[112] + 5.21*x[113] + 10.91*x[114] + 6.69*x[115] + 3.96*x[116] + 5.91*x[117] + 4.83*x[118] + 6.53*x[119] + 4.34*x[120] + 6.94*x[121] + 4.89*x[122] + 8.04*x[123] + 7.04*x[124] + 5.76*x[125] + 7.09*x[126] + 4.58*x[127] + 9.47*x[128] + 3.69*x[129] + 2.43*x[130] + 0.6*x[131] + 0.54*x[132] + 0.25*x[133] + 4.93*x[134] + 3.5*x[135] + 7.77*x[136] + 4.46*x[137] + 3.56*x[138] + 4.24*x[139] + 5.08*x[140] + 6.61*x[141] + 5.07*x[142] + 7.98*x[143] + 4.82*x[144] + 4.22*x[145] + 9.52*x[146] + 2.55*x[147] + 5.27*x[148] + 4.2*x[149] + 3.67*x[150] + 2.55*x[151] + 3.69*x[152] + 4.94*x[153] + 2.45*x[154] + 5.39*x[155] + 3.59*x[156] + 3.26*x[157] + 3.97*x[158] + 4.2*x[159] + 3.6*x[160] + 3.16*x[161] + 3.64*x[162] + 5.01*x[163] + 2.36*x[164] + 1.98*x[165] + 2.76*x[166] + 1.81*x[167] + 1.73*x[168] + 4.8*x[169] + 3.74*x[170] + 2.09*x[171] + 1.94*x[172] + 3.41*x[173] + 4.9*x[174] + 2.43*x[175] + 2.9*x[176] + 3.94*x[177] + 3.63*x[178] + 1.66*x[179] + 1.36*x[180] + 3.83*x[181] + 1.39*x[182] + 3.98*x[183] + 2.4*x[184] + 1.8*x[185] + 2.28*x[186] + 4.02*x[187] + 1.64*x[188] + 0.76*x[189] + 0.39*x[190] + 1.26*x[191] + 1.96*x[192] + 2.64*x[193] + 2.83*x[194] + 2.01*x[195] + 1.97*x[196] + 1.71*x[197] + 1.42*x[198] + 1.19*x[199] + 1.09*x[200] + 2.18*x[201] + 2.14*x[202] + 2.02*x[203] + 2.63*x[204] + 1.56*x[205] + 2.08*x[206] + 0.76*x[207] + 2.05*x[208] + 2.55*x[209] + 1.91*x[210] + 1.43*x[211] + 0.76*x[212] + 0.37*x[213] + 1.83*x[214] + 2.12*x[215] + 1.15*x[216] + 0.33*x[217] + 0.34*x[218] + 1.52*x[219] + 2.74*x[220] + 1.14*x[221] + 0.64*x[222] + 0.34*x[223] + 2.17*x[224] + 1.52*x[225] + 1.35*x[226] + 1.36*x[227] + 1.25*x[228] + 0.56*x[229] + 0.62*x[230] + 0.51*x[231] + 0.15*x[232] + 1.8*x[233] + 0.98*x[234] + 1.11*x[235] + 0.76*x[236] + 0.88*x[237] + 1.05*x[238] + 0.65*x[239] + 0.5*x[240] + 0.82*x[241] + 0.85*x[242] + 0.71*x[243] + 0.25*x[244] + 0.25*x[245] + 0.33*x[246] + 0.31*x[247] + 0.43*x[248] + 0.22*x[249] + 0.33*x[250] + 0.18*x[251] + 0.21*x[252] + 0.27*x[253] + 0.46*x[254] + 0.0*x[255] + 0.0*x[256] + 0.0*x[257] + 0.0*x[258] + 0.0*x[259] + 0.0*x[260] + 0.0*x[261] + 0.0*x[262] + 0.0*x[263] + 0.0*x[264] + 0.0*x[265] + 0.0*x[266] + 0.0*x[267] + 0.0*x[268] + 0.16*x[269] + 0.1*x[270] + 0.0*x[271] + 0.0*x[272] + 0.0*x[273] + 0.0*x[274] + 0.0*x[275] + 0.0*x[276] + 0.0*x[277] + 0.0*x[278] + 0.0*x[279] + 0.0*x[280] + 0.0*x[281] + 0.0*x[282] + 0.0*x[283] + 0.0*x[284] + 0.0*x[285] + 0.0*x[286] + 0.0*x[287] + 0.0*x[288] + 0.0*x[289] + 0.0*x[290] + 0.0*x[291] + 0.0*x[292] + 0.0*x[293] + 0.0*x[294] + 0.0*x[295] + 0.0*x[296] + 0.0*x[297] + 0.0*x[298] + 0.0*x[299] + 0.0*x[300] + 0.0*x[301] + 0.0*x[302] + 0.0*x[303] + 0.0*x[304] + 0.0*x[305] + 0.0*x[306] + 0.0*x[307] + 0.0*x[308] + 0.0*x[309] + 0.0*x[310] + 0.0*x[311] + 0.0*x[312] + 0.0*x[313] + 0.0*x[314] + 0.0*x[315] + 0.0*x[316] + 0.0*x[317] + 0.0*x[318] + 0.0*x[319] + 0.0*x[320] + 0.0*x[321] + 0.0*x[322] + 0.0*x[323] + 0.0*x[324] + 0.0*x[325] + 0.0*x[326] + 0.0*x[327] + 0.0*x[328] + 0.0*x[329] + 0.0*x[330] + 0.0*x[331] + 0.0*x[332] + 0.0*x[333] + 0.0*x[334] + 0.0*x[335] + 0.0*x[336] + 0.0*x[337] + 0.0*x[338] + 0.0*x[339] + 0.0*x[340] + 0.0*x[341] + 0.0*x[342] + 0.0*x[343] + 0.0*x[344] + 0.0*x[345] + 0.0*x[346] + 0.0*x[347] + 0.0*x[348] + 0.0*x[349] + 0.0*x[350] + 0.0*x[351] + 0.0*x[352] + 0.0*x[353] + 0.0*x[354] + 0.0*x[355] + 0.0*x[356] + 0.0*x[357] + 0.0*x[358] + 0.0*x[359] + 0.0*x[360] + 0.0*x[361] + 0.0*x[362] + 0.0*x[363] + 0.0*x[364] + 0.0*x[365] + 0.0*x[366] + 0.0*x[367] + 0.0*x[368] + 0.0*x[369] + 0.0*x[370] + 0.0*x[371] + 0.0*x[372] + 0.0*x[373] + 0.0*x[374] + 0.0*x[375] + 0.0*x[376] + 0.0*x[377] + 0.0*x[378] + 0.0*x[379] + 0.0*x[380] + 0.0*x[381] + 0.0*x[382] + 0.0*x[383] + 0.0*x[384] + 0.0*x[385] + 0.0*x[386] + 0.0*x[387] + 0.0*x[388] + 0.0*x[389] + 0.0*x[390] + 0.0*x[391]
8 Constraint Declarations
BudgetConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : -Inf : 7500*x[0] + 5800*x[1] + 9300*x[2] + 5200*x[3] + 6000*x[4] + 6700*x[5] + 5800*x[6] + 3600*x[7] + 5600*x[8] + 2800*x[9] + 6200*x[10] + 3900*x[11] + 6800*x[12] + 2900*x[13] + 7000*x[14] + 6100*x[15] + 7200*x[16] + 9200*x[17] + 4900*x[18] + 6400*x[19] + 7700*x[20] + 8200*x[21] + 7300*x[22] + 7300*x[23] + 5200*x[24] + 3000*x[25] + 7800*x[26] + 6000*x[27] + 5700*x[28] + 6300*x[29] + 4000*x[30] + 8400*x[31] + 5100*x[32] + 9900*x[33] + 2400*x[34] + 5500*x[35] + 3900*x[36] + 5000*x[37] + 8600*x[38] + 7100*x[39] + 6900*x[40] + 3500*x[41] + 4300*x[42] + 7500*x[43] + 6800*x[44] + 5800*x[45] + 3000*x[46] + 7600*x[47] + 2900*x[48] + 3700*x[49] + 5600*x[50] + 6500*x[51] + 5400*x[52] + 7400*x[53] + 6900*x[54] + 4600*x[55] + 4500*x[56] + 6200*x[57] + 7800*x[58] + 3300*x[59] + 4700*x[60] + 7000*x[61] + 6300*x[62] + 3900*x[63] + 5900*x[64] + 2700*x[65] + 4800*x[66] + 4700*x[67] + 4000*x[68] + 3300*x[69] + 8000*x[70] + 4500*x[71] + 5300*x[72] + 3400*x[73] + 3100*x[74] + 3700*x[75] + 6400*x[76] + 6300*x[77] + 3600*x[78] + 3100*x[79] + 5000*x[80] + 5400*x[81] + 2500*x[82] + 4200*x[83] + 3800*x[84] + 5300*x[85] + 3100*x[86] + 3200*x[87] + 5100*x[88] + 5700*x[89] + 4400*x[90] + 4900*x[91] + 5000*x[92] + 7100*x[93] + 4000*x[94] + 5800*x[95] + 5500*x[96] + 5200*x[97] + 5500*x[98] + 4800*x[99] + 3600*x[100] + 3100*x[101] + 2700*x[102] + 5200*x[103] + 7900*x[104] + 3200*x[105] + 3500*x[106] + 3000*x[107] + 4900*x[108] + 5400*x[109] + 7200*x[110] + 3500*x[111] + 4400*x[112] + 3200*x[113] + 5000*x[114] + 4800*x[115] + 2800*x[116] + 3400*x[117] + 2300*x[118] + 3700*x[119] + 3000*x[120] + 3400*x[121] + 3400*x[122] + 5000*x[123] + 3300*x[124] + 3200*x[125] + 4900*x[126] + 3000*x[127] + 7000*x[128] + 2500*x[129] + 4000*x[130] + 4000*x[131] + 4000*x[132] + 4000*x[133] + 3100*x[134] + 2500*x[135] + 4500*x[136] + 3000*x[137] + 2500*x[138] + 3200*x[139] + 3600*x[140] + 4400*x[141] + 3800*x[142] + 5300*x[143] + 3400*x[144] + 3300*x[145] + 4000*x[146] + 2500*x[147] + 4400*x[148] + 3000*x[149] + 3200*x[150] + 2500*x[151] + 3000*x[152] + 4400*x[153] + 2500*x[154] + 4700*x[155] + 3600*x[156] + 3400*x[157] + 3100*x[158] + 4100*x[159] + 2200*x[160] + 3000*x[161] + 2600*x[162] + 4700*x[163] + 2500*x[164] + 2500*x[165] + 3000*x[166] + 2600*x[167] + 2500*x[168] + 4600*x[169] + 4300*x[170] + 2500*x[171] + 3100*x[172] + 3200*x[173] + 4600*x[174] + 3500*x[175] + 3000*x[176] + 4400*x[177] + 3200*x[178] + 2500*x[179] + 2500*x[180] + 4600*x[181] + 2500*x[182] + 4200*x[183] + 3000*x[184] + 2500*x[185] + 3200*x[186] + 4200*x[187] + 2500*x[188] + 2500*x[189] + 2500*x[190] + 2500*x[191] + 3100*x[192] + 3000*x[193] + 4400*x[194] + 3000*x[195] + 3000*x[196] + 3000*x[197] + 3000*x[198] + 2500*x[199] + 2500*x[200] + 3000*x[201] + 3000*x[202] + 3000*x[203] + 4200*x[204] + 3000*x[205] + 4400*x[206] + 2500*x[207] + 3000*x[208] + 4600*x[209] + 3100*x[210] + 3000*x[211] + 2500*x[212] + 2500*x[213] + 3000*x[214] + 4300*x[215] + 3000*x[216] + 2500*x[217] + 2500*x[218] + 3000*x[219] + 5500*x[220] + 3000*x[221] + 2500*x[222] + 2500*x[223] + 4400*x[224] + 3000*x[225] + 3000*x[226] + 3000*x[227] + 3000*x[228] + 3000*x[229] + 3000*x[230] + 2500*x[231] + 3300*x[232] + 4000*x[233] + 3100*x[234] + 4500*x[235] + 3000*x[236] + 3000*x[237] + 4800*x[238] + 3000*x[239] + 3000*x[240] + 4000*x[241] + 4000*x[242] + 4000*x[243] + 3000*x[244] + 2500*x[245] + 2500*x[246] + 3000*x[247] + 4000*x[248] + 4000*x[249] + 3000*x[250] + 4000*x[251] + 3000*x[252] + 4000*x[253] + 4000*x[254] + 5100*x[255] + 3000*x[256] + 2500*x[257] + 4000*x[258] + 4000*x[259] + 4000*x[260] + 4000*x[261] + 3000*x[262] + 3000*x[263] + 4900*x[264] + 2500*x[265] + 3000*x[266] + 3000*x[267] + 3000*x[268] + 4000*x[269] + 4000*x[270] + 3000*x[271] + 3000*x[272] + 4000*x[273] + 4600*x[274] + 2500*x[275] + 3000*x[276] + 4000*x[277] + 2500*x[278] + 3000*x[279] + 3000*x[280] + 2500*x[281] + 4000*x[282] + 3000*x[283] + 2500*x[284] + 4000*x[285] + 3000*x[286] + 3000*x[287] + 4000*x[288] + 4000*x[289] + 4000*x[290] + 5900*x[291] + 4800*x[292] + 3000*x[293] + 4000*x[294] + 4000*x[295] + 4600*x[296] + 4000*x[297] + 2500*x[298] + 3000*x[299] + 4700*x[300] + 2500*x[301] + 3000*x[302] + 4000*x[303] + 2500*x[304] + 3000*x[305] + 2500*x[306] + 4000*x[307] + 3000*x[308] + 3000*x[309] + 2500*x[310] + 3000*x[311] + 2500*x[312] + 2700*x[313] + 3000*x[314] + 4500*x[315] + 6900*x[316] + 3000*x[317] + 4000*x[318] + 4000*x[319] + 3000*x[320] + 2500*x[321] + 4500*x[322] + 4000*x[323] + 2500*x[324] + 4400*x[325] + 3000*x[326] + 4000*x[327] + 4600*x[328] + 2500*x[329] + 2500*x[330] + 2500*x[331] + 4000*x[332] + 4500*x[333] + 4500*x[334] + 3000*x[335] + 3000*x[336] + 2500*x[337] + 4000*x[338] + 4000*x[339] + 4000*x[340] + 3000*x[341] + 4700*x[342] + 2500*x[343] + 3000*x[344] + 4000*x[345] + 3000*x[346] + 4600*x[347] + 4000*x[348] + 2500*x[349] + 4000*x[350] + 4000*x[351] + 3000*x[352] + 4000*x[353] + 2500*x[354] + 4000*x[355] + 4600*x[356] + 6000*x[357] + 4000*x[358] + 2500*x[359] + 4900*x[360] + 3000*x[361] + 3000*x[362] + 4000*x[363] + 3000*x[364] + 7100*x[365] + 2500*x[366] + 2500*x[367] + 3000*x[368] + 4000*x[369] + 4000*x[370] + 4000*x[371] + 2500*x[372] + 4000*x[373] + 3000*x[374] + 4000*x[375] + 4700*x[376] + 2500*x[377] + 2500*x[378] + 3000*x[379] + 3000*x[380] + 3000*x[381] + 3000*x[382] + 4000*x[383] + 4000*x[384] + 2500*x[385] + 4700*x[386] + 3000*x[387] + 4000*x[388] + 4700*x[389] + 4300*x[390] + 4800*x[391] : 50000.0 : True
DEFConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 1.0 : 0*x[0] + 0*x[1] + 0*x[2] + 0*x[3] + 0*x[4] + 0*x[5] + 0*x[6] + 0*x[7] + 0*x[8] + x[9] + 0*x[10] + 0*x[11] + 0*x[12] + 0*x[13] + 0*x[14] + 0*x[15] + 0*x[16] + 0*x[17] + 0*x[18] + 0*x[19] + 0*x[20] + 0*x[21] + 0*x[22] + 0*x[23] + 0*x[24] + 0*x[25] + 0*x[26] + 0*x[27] + 0*x[28] + 0*x[29] + x[30] + 0*x[31] + 0*x[32] + 0*x[33] + x[34] + 0*x[35] + 0*x[36] + 0*x[37] + 0*x[38] + 0*x[39] + 0*x[40] + x[41] + 0*x[42] + 0*x[43] + 0*x[44] + 0*x[45] + x[46] + 0*x[47] + x[48] + 0*x[49] + 0*x[50] + 0*x[51] + 0*x[52] + 0*x[53] + 0*x[54] + 0*x[55] + 0*x[56] + 0*x[57] + 0*x[58] + 0*x[59] + 0*x[60] + 0*x[61] + 0*x[62] + x[63] + 0*x[64] + x[65] + 0*x[66] + 0*x[67] + 0*x[68] + 0*x[69] + 0*x[70] + 0*x[71] + 0*x[72] + 0*x[73] + 0*x[74] + 0*x[75] + 0*x[76] + 0*x[77] + x[78] + x[79] + 0*x[80] + 0*x[81] + x[82] + 0*x[83] + x[84] + 0*x[85] + 0*x[86] + 0*x[87] + 0*x[88] + 0*x[89] + 0*x[90] + 0*x[91] + 0*x[92] + 0*x[93] + 0*x[94] + 0*x[95] + 0*x[96] + 0*x[97] + 0*x[98] + 0*x[99] + 0*x[100] + 0*x[101] + 0*x[102] + 0*x[103] + 0*x[104] + 0*x[105] + 0*x[106] + 0*x[107] + 0*x[108] + 0*x[109] + 0*x[110] + 0*x[111] + x[112] + 0*x[113] + 0*x[114] + 0*x[115] + 0*x[116] + 0*x[117] + x[118] + x[119] + 0*x[120] + x[121] + 0*x[122] + 0*x[123] + x[124] + x[125] + 0*x[126] + 0*x[127] + 0*x[128] + 0*x[129] + 0*x[130] + 0*x[131] + 0*x[132] + 0*x[133] + 0*x[134] + 0*x[135] + 0*x[136] + 0*x[137] + 0*x[138] + 0*x[139] + 0*x[140] + 0*x[141] + 0*x[142] + 0*x[143] + 0*x[144] + 0*x[145] + 0*x[146] + 0*x[147] + 0*x[148] + 0*x[149] + 0*x[150] + 0*x[151] + 0*x[152] + 0*x[153] + 0*x[154] + 0*x[155] + 0*x[156] + 0*x[157] + 0*x[158] + 0*x[159] + x[160] + 0*x[161] + x[162] + 0*x[163] + 0*x[164] + 0*x[165] + 0*x[166] + 0*x[167] + 0*x[168] + 0*x[169] + 0*x[170] + 0*x[171] + 0*x[172] + 0*x[173] + 0*x[174] + 0*x[175] + 0*x[176] + 0*x[177] + 0*x[178] + 0*x[179] + 0*x[180] + 0*x[181] + 0*x[182] + 0*x[183] + 0*x[184] + 0*x[185] + 0*x[186] + 0*x[187] + 0*x[188] + 0*x[189] + 0*x[190] + 0*x[191] + 0*x[192] + 0*x[193] + 0*x[194] + 0*x[195] + 0*x[196] + 0*x[197] + 0*x[198] + 0*x[199] + 0*x[200] + 0*x[201] + 0*x[202] + 0*x[203] + 0*x[204] + 0*x[205] + 0*x[206] + 0*x[207] + 0*x[208] + 0*x[209] + 0*x[210] + 0*x[211] + 0*x[212] + 0*x[213] + 0*x[214] + 0*x[215] + 0*x[216] + 0*x[217] + 0*x[218] + 0*x[219] + 0*x[220] + 0*x[221] + 0*x[222] + 0*x[223] + 0*x[224] + 0*x[225] + 0*x[226] + 0*x[227] + 0*x[228] + 0*x[229] + 0*x[230] + 0*x[231] + 0*x[232] + 0*x[233] + 0*x[234] + 0*x[235] + 0*x[236] + 0*x[237] + 0*x[238] + 0*x[239] + 0*x[240] + 0*x[241] + 0*x[242] + 0*x[243] + 0*x[244] + 0*x[245] + 0*x[246] + 0*x[247] + 0*x[248] + 0*x[249] + 0*x[250] + 0*x[251] + 0*x[252] + 0*x[253] + 0*x[254] + 0*x[255] + 0*x[256] + 0*x[257] + 0*x[258] + 0*x[259] + 0*x[260] + 0*x[261] + 0*x[262] + 0*x[263] + 0*x[264] + 0*x[265] + 0*x[266] + 0*x[267] + 0*x[268] + 0*x[269] + 0*x[270] + 0*x[271] + 0*x[272] + 0*x[273] + 0*x[274] + 0*x[275] + 0*x[276] + 0*x[277] + 0*x[278] + 0*x[279] + 0*x[280] + 0*x[281] + 0*x[282] + 0*x[283] + 0*x[284] + 0*x[285] + 0*x[286] + 0*x[287] + 0*x[288] + 0*x[289] + 0*x[290] + 0*x[291] + 0*x[292] + 0*x[293] + 0*x[294] + 0*x[295] + 0*x[296] + 0*x[297] + 0*x[298] + 0*x[299] + 0*x[300] + 0*x[301] + 0*x[302] + 0*x[303] + 0*x[304] + 0*x[305] + 0*x[306] + 0*x[307] + 0*x[308] + 0*x[309] + 0*x[310] + 0*x[311] + 0*x[312] + 0*x[313] + 0*x[314] + 0*x[315] + 0*x[316] + 0*x[317] + 0*x[318] + 0*x[319] + 0*x[320] + 0*x[321] + 0*x[322] + 0*x[323] + 0*x[324] + 0*x[325] + 0*x[326] + 0*x[327] + 0*x[328] + 0*x[329] + 0*x[330] + 0*x[331] + 0*x[332] + 0*x[333] + 0*x[334] + 0*x[335] + 0*x[336] + 0*x[337] + 0*x[338] + 0*x[339] + 0*x[340] + 0*x[341] + 0*x[342] + 0*x[343] + 0*x[344] + 0*x[345] + 0*x[346] + 0*x[347] + 0*x[348] + 0*x[349] + 0*x[350] + 0*x[351] + 0*x[352] + 0*x[353] + 0*x[354] + 0*x[355] + 0*x[356] + 0*x[357] + 0*x[358] + 0*x[359] + 0*x[360] + 0*x[361] + 0*x[362] + 0*x[363] + 0*x[364] + 0*x[365] + 0*x[366] + 0*x[367] + 0*x[368] + 0*x[369] + 0*x[370] + 0*x[371] + 0*x[372] + 0*x[373] + 0*x[374] + 0*x[375] + 0*x[376] + 0*x[377] + 0*x[378] + 0*x[379] + 0*x[380] + 0*x[381] + 0*x[382] + 0*x[383] + 0*x[384] + 0*x[385] + 0*x[386] + 0*x[387] + 0*x[388] + 0*x[389] + 0*x[390] + 0*x[391] : 1.0 : True
QBConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 1.0 : 0*x[0] + 0*x[1] + 0*x[2] + 0*x[3] + x[4] + 0*x[5] + 0*x[6] + 0*x[7] + 0*x[8] + 0*x[9] + 0*x[10] + 0*x[11] + 0*x[12] + 0*x[13] + 0*x[14] + 0*x[15] + 0*x[16] + 0*x[17] + 0*x[18] + 0*x[19] + 0*x[20] + x[21] + 0*x[22] + 0*x[23] + 0*x[24] + 0*x[25] + 0*x[26] + 0*x[27] + 0*x[28] + 0*x[29] + 0*x[30] + 0*x[31] + 0*x[32] + 0*x[33] + 0*x[34] + 0*x[35] + 0*x[36] + 0*x[37] + 0*x[38] + 0*x[39] + 0*x[40] + 0*x[41] + 0*x[42] + 0*x[43] + x[44] + 0*x[45] + 0*x[46] + 0*x[47] + 0*x[48] + 0*x[49] + 0*x[50] + 0*x[51] + 0*x[52] + 0*x[53] + 0*x[54] + 0*x[55] + 0*x[56] + x[57] + x[58] + 0*x[59] + 0*x[60] + x[61] + x[62] + 0*x[63] + 0*x[64] + 0*x[65] + 0*x[66] + 0*x[67] + 0*x[68] + 0*x[69] + x[70] + 0*x[71] + 0*x[72] + 0*x[73] + 0*x[74] + 0*x[75] + x[76] + 0*x[77] + 0*x[78] + 0*x[79] + 0*x[80] + 0*x[81] + 0*x[82] + 0*x[83] + 0*x[84] + 0*x[85] + 0*x[86] + 0*x[87] + 0*x[88] + x[89] + 0*x[90] + x[91] + x[92] + 0*x[93] + 0*x[94] + x[95] + x[96] + x[97] + 0*x[98] + x[99] + 0*x[100] + 0*x[101] + 0*x[102] + 0*x[103] + x[104] + 0*x[105] + 0*x[106] + 0*x[107] + 0*x[108] + x[109] + 0*x[110] + 0*x[111] + 0*x[112] + 0*x[113] + x[114] + 0*x[115] + 0*x[116] + 0*x[117] + 0*x[118] + 0*x[119] + 0*x[120] + 0*x[121] + 0*x[122] + 0*x[123] + 0*x[124] + 0*x[125] + 0*x[126] + 0*x[127] + 0*x[128] + 0*x[129] + 0*x[130] + 0*x[131] + 0*x[132] + 0*x[133] + 0*x[134] + 0*x[135] + 0*x[136] + 0*x[137] + 0*x[138] + 0*x[139] + 0*x[140] + 0*x[141] + 0*x[142] + 0*x[143] + 0*x[144] + 0*x[145] + x[146] + 0*x[147] + 0*x[148] + 0*x[149] + 0*x[150] + 0*x[151] + 0*x[152] + 0*x[153] + 0*x[154] + 0*x[155] + 0*x[156] + 0*x[157] + 0*x[158] + 0*x[159] + 0*x[160] + 0*x[161] + 0*x[162] + 0*x[163] + 0*x[164] + 0*x[165] + 0*x[166] + 0*x[167] + 0*x[168] + 0*x[169] + 0*x[170] + 0*x[171] + 0*x[172] + 0*x[173] + 0*x[174] + 0*x[175] + 0*x[176] + 0*x[177] + 0*x[178] + 0*x[179] + 0*x[180] + 0*x[181] + 0*x[182] + 0*x[183] + 0*x[184] + 0*x[185] + 0*x[186] + 0*x[187] + 0*x[188] + 0*x[189] + 0*x[190] + 0*x[191] + 0*x[192] + 0*x[193] + 0*x[194] + 0*x[195] + 0*x[196] + 0*x[197] + 0*x[198] + 0*x[199] + 0*x[200] + 0*x[201] + 0*x[202] + 0*x[203] + 0*x[204] + 0*x[205] + 0*x[206] + 0*x[207] + 0*x[208] + 0*x[209] + 0*x[210] + 0*x[211] + 0*x[212] + 0*x[213] + 0*x[214] + 0*x[215] + 0*x[216] + 0*x[217] + 0*x[218] + 0*x[219] + 0*x[220] + 0*x[221] + 0*x[222] + 0*x[223] + 0*x[224] + 0*x[225] + 0*x[226] + 0*x[227] + 0*x[228] + 0*x[229] + 0*x[230] + 0*x[231] + 0*x[232] + 0*x[233] + 0*x[234] + 0*x[235] + 0*x[236] + 0*x[237] + x[238] + 0*x[239] + 0*x[240] + 0*x[241] + 0*x[242] + 0*x[243] + 0*x[244] + 0*x[245] + 0*x[246] + 0*x[247] + 0*x[248] + 0*x[249] + 0*x[250] + 0*x[251] + 0*x[252] + 0*x[253] + 0*x[254] + x[255] + 0*x[256] + 0*x[257] + x[258] + 0*x[259] + 0*x[260] + x[261] + 0*x[262] + 0*x[263] + x[264] + 0*x[265] + 0*x[266] + 0*x[267] + 0*x[268] + 0*x[269] + 0*x[270] + 0*x[271] + 0*x[272] + 0*x[273] + x[274] + 0*x[275] + 0*x[276] + 0*x[277] + 0*x[278] + 0*x[279] + 0*x[280] + 0*x[281] + x[282] + 0*x[283] + 0*x[284] + 0*x[285] + 0*x[286] + 0*x[287] + x[288] + 0*x[289] + 0*x[290] + 0*x[291] + x[292] + 0*x[293] + x[294] + x[295] + x[296] + 0*x[297] + 0*x[298] + 0*x[299] + x[300] + 0*x[301] + 0*x[302] + 0*x[303] + 0*x[304] + 0*x[305] + 0*x[306] + 0*x[307] + 0*x[308] + 0*x[309] + 0*x[310] + 0*x[311] + 0*x[312] + 0*x[313] + 0*x[314] + x[315] + 0*x[316] + 0*x[317] + x[318] + 0*x[319] + 0*x[320] + 0*x[321] + x[322] + x[323] + 0*x[324] + 0*x[325] + 0*x[326] + 0*x[327] + x[328] + 0*x[329] + 0*x[330] + 0*x[331] + 0*x[332] + x[333] + x[334] + 0*x[335] + 0*x[336] + 0*x[337] + x[338] + 0*x[339] + 0*x[340] + 0*x[341] + x[342] + 0*x[343] + 0*x[344] + 0*x[345] + 0*x[346] + x[347] + 0*x[348] + 0*x[349] + 0*x[350] + x[351] + 0*x[352] + x[353] + 0*x[354] + x[355] + x[356] + 0*x[357] + 0*x[358] + 0*x[359] + x[360] + 0*x[361] + 0*x[362] + 0*x[363] + 0*x[364] + x[365] + 0*x[366] + 0*x[367] + 0*x[368] + 0*x[369] + 0*x[370] + x[371] + 0*x[372] + 0*x[373] + 0*x[374] + 0*x[375] + x[376] + 0*x[377] + 0*x[378] + 0*x[379] + 0*x[380] + 0*x[381] + 0*x[382] + 0*x[383] + x[384] + 0*x[385] + x[386] + 0*x[387] + 0*x[388] + x[389] + 0*x[390] + 0*x[391] : 1.0 : True
RBConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : -Inf : x[0] + x[1] + x[2] + x[3] + 0*x[4] + x[5] + 0*x[6] + 0*x[7] + 0*x[8] + 0*x[9] + 0*x[10] + 0*x[11] + x[12] + 0*x[13] + x[14] + 0*x[15] + 0*x[16] + 0*x[17] + 0*x[18] + x[19] + 0*x[20] + 0*x[21] + x[22] + 0*x[23] + 0*x[24] + 0*x[25] + 0*x[26] + 0*x[27] + x[28] + x[29] + 0*x[30] + 0*x[31] + 0*x[32] + 0*x[33] + 0*x[34] + x[35] + 0*x[36] + 0*x[37] + x[38] + 0*x[39] + 0*x[40] + 0*x[41] + 0*x[42] + 0*x[43] + 0*x[44] + 0*x[45] + 0*x[46] + 0*x[47] + 0*x[48] + 0*x[49] + x[50] + x[51] + 0*x[52] + 0*x[53] + x[54] + 0*x[55] + 0*x[56] + 0*x[57] + 0*x[58] + 0*x[59] + 0*x[60] + 0*x[61] + 0*x[62] + 0*x[63] + 0*x[64] + 0*x[65] + 0*x[66] + 0*x[67] + 0*x[68] + 0*x[69] + 0*x[70] + 0*x[71] + 0*x[72] + 0*x[73] + 0*x[74] + 0*x[75] + 0*x[76] + 0*x[77] + 0*x[78] + 0*x[79] + x[80] + x[81] + 0*x[82] + 0*x[83] + 0*x[84] + 0*x[85] + 0*x[86] + 0*x[87] + x[88] + 0*x[89] + 0*x[90] + 0*x[91] + 0*x[92] + x[93] + 0*x[94] + 0*x[95] + 0*x[96] + 0*x[97] + 0*x[98] + 0*x[99] + 0*x[100] + 0*x[101] + 0*x[102] + 0*x[103] + 0*x[104] + 0*x[105] + 0*x[106] + 0*x[107] + 0*x[108] + 0*x[109] + x[110] + 0*x[111] + 0*x[112] + 0*x[113] + 0*x[114] + x[115] + 0*x[116] + 0*x[117] + 0*x[118] + 0*x[119] + 0*x[120] + 0*x[121] + 0*x[122] + x[123] + 0*x[124] + 0*x[125] + x[126] + 0*x[127] + 0*x[128] + 0*x[129] + x[130] + x[131] + x[132] + x[133] + 0*x[134] + 0*x[135] + x[136] + 0*x[137] + 0*x[138] + 0*x[139] + 0*x[140] + x[141] + 0*x[142] + x[143] + 0*x[144] + 0*x[145] + 0*x[146] + 0*x[147] + x[148] + 0*x[149] + 0*x[150] + 0*x[151] + 0*x[152] + x[153] + 0*x[154] + x[155] + 0*x[156] + 0*x[157] + 0*x[158] + 0*x[159] + 0*x[160] + 0*x[161] + 0*x[162] + x[163] + 0*x[164] + 0*x[165] + 0*x[166] + 0*x[167] + 0*x[168] + x[169] + x[170] + 0*x[171] + 0*x[172] + 0*x[173] + x[174] + 0*x[175] + 0*x[176] + x[177] + 0*x[178] + 0*x[179] + 0*x[180] + x[181] + 0*x[182] + x[183] + 0*x[184] + 0*x[185] + 0*x[186] + x[187] + 0*x[188] + 0*x[189] + 0*x[190] + 0*x[191] + 0*x[192] + 0*x[193] + x[194] + 0*x[195] + 0*x[196] + 0*x[197] + 0*x[198] + 0*x[199] + 0*x[200] + 0*x[201] + 0*x[202] + 0*x[203] + x[204] + 0*x[205] + x[206] + 0*x[207] + 0*x[208] + x[209] + 0*x[210] + 0*x[211] + 0*x[212] + 0*x[213] + 0*x[214] + x[215] + 0*x[216] + 0*x[217] + 0*x[218] + 0*x[219] + 0*x[220] + 0*x[221] + 0*x[222] + 0*x[223] + x[224] + 0*x[225] + 0*x[226] + 0*x[227] + 0*x[228] + 0*x[229] + 0*x[230] + 0*x[231] + 0*x[232] + x[233] + 0*x[234] + x[235] + 0*x[236] + 0*x[237] + 0*x[238] + 0*x[239] + 0*x[240] + x[241] + x[242] + x[243] + 0*x[244] + 0*x[245] + 0*x[246] + 0*x[247] + x[248] + x[249] + 0*x[250] + x[251] + 0*x[252] + x[253] + x[254] + 0*x[255] + 0*x[256] + 0*x[257] + 0*x[258] + x[259] + x[260] + 0*x[261] + 0*x[262] + 0*x[263] + 0*x[264] + 0*x[265] + 0*x[266] + 0*x[267] + 0*x[268] + x[269] + x[270] + 0*x[271] + 0*x[272] + x[273] + 0*x[274] + 0*x[275] + 0*x[276] + x[277] + 0*x[278] + 0*x[279] + 0*x[280] + 0*x[281] + 0*x[282] + 0*x[283] + 0*x[284] + x[285] + 0*x[286] + 0*x[287] + 0*x[288] + x[289] + x[290] + x[291] + 0*x[292] + 0*x[293] + 0*x[294] + 0*x[295] + 0*x[296] + x[297] + 0*x[298] + 0*x[299] + 0*x[300] + 0*x[301] + 0*x[302] + x[303] + 0*x[304] + 0*x[305] + 0*x[306] + x[307] + 0*x[308] + 0*x[309] + 0*x[310] + 0*x[311] + 0*x[312] + 0*x[313] + 0*x[314] + 0*x[315] + x[316] + 0*x[317] + 0*x[318] + x[319] + 0*x[320] + 0*x[321] + 0*x[322] + 0*x[323] + 0*x[324] + x[325] + 0*x[326] + x[327] + 0*x[328] + 0*x[329] + 0*x[330] + 0*x[331] + x[332] + 0*x[333] + 0*x[334] + 0*x[335] + 0*x[336] + 0*x[337] + 0*x[338] + x[339] + x[340] + 0*x[341] + 0*x[342] + 0*x[343] + 0*x[344] + x[345] + 0*x[346] + 0*x[347] + x[348] + 0*x[349] + x[350] + 0*x[351] + 0*x[352] + 0*x[353] + 0*x[354] + 0*x[355] + 0*x[356] + x[357] + x[358] + 0*x[359] + 0*x[360] + 0*x[361] + 0*x[362] + x[363] + 0*x[364] + 0*x[365] + 0*x[366] + 0*x[367] + 0*x[368] + x[369] + x[370] + 0*x[371] + 0*x[372] + x[373] + 0*x[374] + x[375] + 0*x[376] + 0*x[377] + 0*x[378] + 0*x[379] + 0*x[380] + 0*x[381] + 0*x[382] + x[383] + 0*x[384] + 0*x[385] + 0*x[386] + 0*x[387] + x[388] + 0*x[389] + x[390] + 0*x[391] : 3.0 : True
RSTConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 6.0 : (24.92*x[0] + 24.17*x[1] + 23.33*x[2] + 20.82*x[3] + 15.14*x[4] + 15.07*x[5] + 14.88*x[6] + 14.21*x[7] + 13.42*x[8] + 13.38*x[9] + 12.79*x[10] + 12.73*x[11] + 12.63*x[12] + 12.12*x[13] + 12.01*x[14] + 11.91*x[15] + 11.85*x[16] + 11.76*x[17] + 11.53*x[18] + 11.37*x[19] + 11.21*x[20] + 11.16*x[21] + 11.08*x[22] + 10.8*x[23] + 10.64*x[24] + 10.28*x[25] + 10.12*x[26] + 10.04*x[27] + 10.02*x[28] + 10.02*x[29] + 9.95*x[30] + 9.94*x[31] + 9.57*x[32] + 9.54*x[33] + 9.52*x[34] + 9.38*x[35] + 9.19*x[36] + 9.18*x[37] + 8.85*x[38] + 8.47*x[39] + 8.24*x[40] + 8.1*x[41] + 8.06*x[42] + 8.02*x[43] + 7.88*x[44] + 7.67*x[45] + 7.54*x[46] + 7.47*x[47] + 7.18*x[48] + 7.17*x[49] + 7.12*x[50] + 6.8*x[51] + 6.79*x[52] + 6.78*x[53] + 6.77*x[54] + 6.73*x[55] + 6.47*x[56] + 6.46*x[57] + 6.33*x[58] + 6.26*x[59] + 6.24*x[60] + 5.95*x[61] + 5.85*x[62] + 5.85*x[63] + 5.84*x[64] + 5.78*x[65] + 5.76*x[66] + 5.66*x[67] + 5.49*x[68] + 5.46*x[69] + 5.42*x[70] + 5.39*x[71] + 5.23*x[72] + 5.18*x[73] + 5.18*x[74] + 4.92*x[75] + 4.9*x[76] + 4.73*x[77] + 4.69*x[78] + 4.69*x[79] + 4.64*x[80] + 4.6*x[81] + 4.56*x[82] + 4.56*x[83] + 4.45*x[84] + 4.45*x[85] + 4.41*x[86] + 4.35*x[87] + 4.3*x[88] + 4.29*x[89] + 4.28*x[90] + 4.25*x[91] + 4.17*x[92] + 4.01*x[93] + 3.9*x[94] + 3.76*x[95] + 3.76*x[96] + 3.74*x[97] + 3.72*x[98] + 3.54*x[99] + 3.48*x[100] + 3.47*x[101] + 3.12*x[102] + 3.12*x[103] + 2.94*x[104] + 2.9*x[105] + 2.86*x[106] + 2.85*x[107] + 2.81*x[108] + 2.8*x[109] + 2.65*x[110] + 2.58*x[111] + 2.57*x[112] + 2.52*x[113] + 2.43*x[114] + 2.42*x[115] + 2.41*x[116] + 2.32*x[117] + 2.29*x[118] + 2.28*x[119] + 2.24*x[120] + 2.15*x[121] + 2.09*x[122] + 2.07*x[123] + 2.03*x[124] + 1.97*x[125] + 1.96*x[126] + 1.92*x[127] + 1.87*x[128] + 1.8*x[129] + 1.79*x[130] + 1.79*x[131] + 1.79*x[132] + 1.79*x[133] + 1.73*x[134] + 1.69*x[135] + 1.62*x[136] + 1.55*x[137] + 1.49*x[138] + 1.46*x[139] + 1.41*x[140] + 1.39*x[141] + 1.37*x[142] + 1.34*x[143] + 1.3*x[144] + 1.24*x[145] + 1.18*x[146] + 0.92*x[147] + 0.91*x[148] + 0.89*x[149] + 0.85*x[150] + 0.85*x[151] + 0.83*x[152] + 0.69*x[153] + 0.67*x[154] + 0.63*x[155] + 0.57*x[156] + 0.56*x[157] + 0.53*x[158] + 0.52*x[159] + 0.5*x[160] + 0.45*x[161] + 0.44*x[162] + 0.42*x[163] + 0.4*x[164] + 0.38*x[165] + 0.35*x[166] + 0.35*x[167] + 0.34*x[168] + 0.32*x[169] + 0.31*x[170] + 0.31*x[171] + 0.29*x[172] + 0.28*x[173] + 0.28*x[174] + 0.27*x[175] + 0.22*x[176] + 0.22*x[177] + 0.21*x[178] + 0.21*x[179] + 0.2*x[180] + 0.19*x[181] + 0.16*x[182] + 0.15*x[183] + 0.15*x[184] + 0.15*x[185] + 0.14*x[186] + 0.13*x[187] + 0.13*x[188] + 0.12*x[189] + 0.12*x[190] + 0.11*x[191] + 0.09*x[192] + 0.08*x[193] + 0.08*x[194] + 0.07*x[195] + 0.07*x[196] + 0.07*x[197] + 0.07*x[198] + 0.07*x[199] + 0.07*x[200] + 0.06*x[201] + 0.06*x[202] + 0.06*x[203] + 0.05*x[204] + 0.05*x[205] + 0.05*x[206] + 0.05*x[207] + 0.04*x[208] + 0.04*x[209] + 0.04*x[210] + 0.04*x[211] + 0.04*x[212] + 0.04*x[213] + 0.03*x[214] + 0.03*x[215] + 0.03*x[216] + 0.03*x[217] + 0.03*x[218] + 0.02*x[219] + 0.02*x[220] + 0.02*x[221] + 0.02*x[222] + 0.02*x[223] + 0.01*x[224] + 0.01*x[225] + 0.01*x[226] + 0.01*x[227] + 0.01*x[228] + 0.01*x[229] + 0.01*x[230] + 0.01*x[231] + 0.01*x[232] + 0.0*x[233] + 0.0*x[234] + 0.0*x[235] + 0.0*x[236] + 0.0*x[237] + 0.0*x[238] + 0.0*x[239] + 0.0*x[240] + 0.0*x[241] + 0.0*x[242] + 0.0*x[243] + 0.0*x[244] + 0.0*x[245] + 0.0*x[246] + 0.0*x[247] + 0.0*x[248] + 0.0*x[249] + 0.0*x[250] + 0.0*x[251] + 0.0*x[252] + 0.0*x[253] + 0.0*x[254] + 0.0*x[255] + 0.0*x[256] + 0.0*x[257] + 0.0*x[258] + 0.0*x[259] + 0.0*x[260] + 0.0*x[261] + 0.0*x[262] + 0.0*x[263] + 0.0*x[264] + 0.0*x[265] + 0.0*x[266] + 0.0*x[267] + 0.0*x[268] + 0.0*x[269] + 0.0*x[270] + 0.0*x[271] + 0.0*x[272] + 0.0*x[273] + 0.0*x[274] + 0.0*x[275] + 0.0*x[276] + 0.0*x[277] + 0.0*x[278] + 0.0*x[279] + 0.0*x[280] + 0.0*x[281] + 0.0*x[282] + 0.0*x[283] + 0.0*x[284] + 0.0*x[285] + 0.0*x[286] + 0.0*x[287] + 0.0*x[288] + 0.0*x[289] + 0.0*x[290] + 0.0*x[291] + 0.0*x[292] + 0.0*x[293] + 0.0*x[294] + 0.0*x[295] + 0.0*x[296] + 0.0*x[297] + 0.0*x[298] + 0.0*x[299] + 0.0*x[300] + 0.0*x[301] + 0.0*x[302] + 0.0*x[303] + 0.0*x[304] + 0.0*x[305] + 0.0*x[306] + 0.0*x[307] + 0.0*x[308] + 0.0*x[309] + 0.0*x[310] + 0.0*x[311] + 0.0*x[312] + 0.0*x[313] + 0.0*x[314] + 0.0*x[315] + 0.0*x[316] + 0.0*x[317] + 0.0*x[318] + 0.0*x[319] + 0.0*x[320] + 0.0*x[321] + 0.0*x[322] + 0.0*x[323] + 0.0*x[324] + 0.0*x[325] + 0.0*x[326] + 0.0*x[327] + 0.0*x[328] + 0.0*x[329] + 0.0*x[330] + 0.0*x[331] + 0.0*x[332] + 0.0*x[333] + 0.0*x[334] + 0.0*x[335] + 0.0*x[336] + 0.0*x[337] + 0.0*x[338] + 0.0*x[339] + 0.0*x[340] + 0.0*x[341] + 0.0*x[342] + 0.0*x[343] + 0.0*x[344] + 0.0*x[345] + 0.0*x[346] + 0.0*x[347] + 0.0*x[348] + 0.0*x[349] + 0.0*x[350] + 0.0*x[351] + 0.0*x[352] + 0.0*x[353] + 0.0*x[354] + 0.0*x[355] + 0.0*x[356] + 0.0*x[357] + 0.0*x[358] + 0.0*x[359] + 0.0*x[360] + 0.0*x[361] + 0.0*x[362] + 0.0*x[363] + 0.0*x[364] + 0.0*x[365] + 0.0*x[366] + 0.0*x[367] + 0.0*x[368] + 0.0*x[369] + 0.0*x[370] + 0.0*x[371] + 0.0*x[372] + 0.0*x[373] + 0.0*x[374] + 0.0*x[375] + 0.0*x[376] + 0.0*x[377] + 0.0*x[378] + 0.0*x[379] + 0.0*x[380] + 0.0*x[381] + 0.0*x[382] + 0.0*x[383] + 0.0*x[384] + 0.0*x[385] + 0.0*x[386] + 0.0*x[387] + 0.0*x[388] + 0.0*x[389] + 0.0*x[390] + 0.0*x[391])/9 : +Inf : True
TEConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : -Inf : 0*x[0] + 0*x[1] + 0*x[2] + 0*x[3] + 0*x[4] + 0*x[5] + 0*x[6] + 0*x[7] + 0*x[8] + 0*x[9] + 0*x[10] + 0*x[11] + 0*x[12] + x[13] + 0*x[14] + 0*x[15] + 0*x[16] + 0*x[17] + 0*x[18] + 0*x[19] + 0*x[20] + 0*x[21] + 0*x[22] + 0*x[23] + x[24] + x[25] + 0*x[26] + 0*x[27] + 0*x[28] + 0*x[29] + 0*x[30] + 0*x[31] + 0*x[32] + 0*x[33] + 0*x[34] + 0*x[35] + 0*x[36] + 0*x[37] + 0*x[38] + 0*x[39] + 0*x[40] + 0*x[41] + 0*x[42] + 0*x[43] + 0*x[44] + x[45] + 0*x[46] + x[47] + 0*x[48] + x[49] + 0*x[50] + 0*x[51] + 0*x[52] + 0*x[53] + 0*x[54] + 0*x[55] + 0*x[56] + 0*x[57] + 0*x[58] + 0*x[59] + 0*x[60] + 0*x[61] + 0*x[62] + 0*x[63] + 0*x[64] + 0*x[65] + x[66] + x[67] + x[68] + 0*x[69] + 0*x[70] + x[71] + 0*x[72] + 0*x[73] + 0*x[74] + 0*x[75] + 0*x[76] + 0*x[77] + 0*x[78] + 0*x[79] + 0*x[80] + 0*x[81] + 0*x[82] + 0*x[83] + 0*x[84] + x[85] + x[86] + x[87] + 0*x[88] + 0*x[89] + x[90] + 0*x[91] + 0*x[92] + 0*x[93] + 0*x[94] + 0*x[95] + 0*x[96] + 0*x[97] + 0*x[98] + 0*x[99] + x[100] + 0*x[101] + x[102] + 0*x[103] + 0*x[104] + x[105] + 0*x[106] + 0*x[107] + x[108] + 0*x[109] + 0*x[110] + 0*x[111] + 0*x[112] + 0*x[113] + 0*x[114] + 0*x[115] + x[116] + 0*x[117] + 0*x[118] + 0*x[119] + x[120] + 0*x[121] + 0*x[122] + 0*x[123] + 0*x[124] + 0*x[125] + 0*x[126] + 0*x[127] + 0*x[128] + x[129] + 0*x[130] + 0*x[131] + 0*x[132] + 0*x[133] + 0*x[134] + x[135] + 0*x[136] + 0*x[137] + x[138] + 0*x[139] + 0*x[140] + 0*x[141] + 0*x[142] + 0*x[143] + 0*x[144] + 0*x[145] + 0*x[146] + x[147] + 0*x[148] + 0*x[149] + 0*x[150] + x[151] + 0*x[152] + 0*x[153] + x[154] + 0*x[155] + 0*x[156] + 0*x[157] + 0*x[158] + 0*x[159] + 0*x[160] + 0*x[161] + 0*x[162] + 0*x[163] + x[164] + x[165] + 0*x[166] + x[167] + x[168] + 0*x[169] + 0*x[170] + x[171] + x[172] + 0*x[173] + 0*x[174] + 0*x[175] + 0*x[176] + 0*x[177] + 0*x[178] + x[179] + x[180] + 0*x[181] + x[182] + 0*x[183] + 0*x[184] + x[185] + 0*x[186] + 0*x[187] + x[188] + x[189] + x[190] + x[191] + 0*x[192] + 0*x[193] + 0*x[194] + 0*x[195] + 0*x[196] + 0*x[197] + 0*x[198] + x[199] + x[200] + 0*x[201] + 0*x[202] + 0*x[203] + 0*x[204] + 0*x[205] + 0*x[206] + x[207] + 0*x[208] + 0*x[209] + 0*x[210] + 0*x[211] + x[212] + x[213] + 0*x[214] + 0*x[215] + 0*x[216] + x[217] + x[218] + 0*x[219] + x[220] + 0*x[221] + x[222] + x[223] + 0*x[224] + 0*x[225] + 0*x[226] + 0*x[227] + 0*x[228] + 0*x[229] + 0*x[230] + x[231] + x[232] + 0*x[233] + 0*x[234] + 0*x[235] + 0*x[236] + 0*x[237] + 0*x[238] + 0*x[239] + 0*x[240] + 0*x[241] + 0*x[242] + 0*x[243] + 0*x[244] + x[245] + x[246] + 0*x[247] + 0*x[248] + 0*x[249] + 0*x[250] + 0*x[251] + 0*x[252] + 0*x[253] + 0*x[254] + 0*x[255] + 0*x[256] + x[257] + 0*x[258] + 0*x[259] + 0*x[260] + 0*x[261] + 0*x[262] + 0*x[263] + 0*x[264] + x[265] + 0*x[266] + 0*x[267] + 0*x[268] + 0*x[269] + 0*x[270] + 0*x[271] + 0*x[272] + 0*x[273] + 0*x[274] + x[275] + 0*x[276] + 0*x[277] + x[278] + 0*x[279] + 0*x[280] + x[281] + 0*x[282] + 0*x[283] + x[284] + 0*x[285] + 0*x[286] + 0*x[287] + 0*x[288] + 0*x[289] + 0*x[290] + 0*x[291] + 0*x[292] + 0*x[293] + 0*x[294] + 0*x[295] + 0*x[296] + 0*x[297] + x[298] + 0*x[299] + 0*x[300] + x[301] + 0*x[302] + 0*x[303] + x[304] + 0*x[305] + x[306] + 0*x[307] + 0*x[308] + 0*x[309] + x[310] + 0*x[311] + x[312] + x[313] + 0*x[314] + 0*x[315] + 0*x[316] + 0*x[317] + 0*x[318] + 0*x[319] + 0*x[320] + x[321] + 0*x[322] + 0*x[323] + x[324] + 0*x[325] + 0*x[326] + 0*x[327] + 0*x[328] + x[329] + x[330] + x[331] + 0*x[332] + 0*x[333] + 0*x[334] + 0*x[335] + 0*x[336] + x[337] + 0*x[338] + 0*x[339] + 0*x[340] + 0*x[341] + 0*x[342] + x[343] + 0*x[344] + 0*x[345] + 0*x[346] + 0*x[347] + 0*x[348] + x[349] + 0*x[350] + 0*x[351] + 0*x[352] + 0*x[353] + x[354] + 0*x[355] + 0*x[356] + 0*x[357] + 0*x[358] + x[359] + 0*x[360] + 0*x[361] + 0*x[362] + 0*x[363] + 0*x[364] + 0*x[365] + x[366] + x[367] + 0*x[368] + 0*x[369] + 0*x[370] + 0*x[371] + x[372] + 0*x[373] + 0*x[374] + 0*x[375] + 0*x[376] + x[377] + x[378] + 0*x[379] + 0*x[380] + 0*x[381] + 0*x[382] + 0*x[383] + 0*x[384] + x[385] + 0*x[386] + 0*x[387] + 0*x[388] + 0*x[389] + 0*x[390] + 0*x[391] : 2.0 : True
WRConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : -Inf : 0*x[0] + 0*x[1] + 0*x[2] + 0*x[3] + 0*x[4] + 0*x[5] + x[6] + x[7] + x[8] + 0*x[9] + x[10] + x[11] + 0*x[12] + 0*x[13] + 0*x[14] + x[15] + x[16] + x[17] + x[18] + 0*x[19] + x[20] + 0*x[21] + 0*x[22] + x[23] + 0*x[24] + 0*x[25] + x[26] + x[27] + 0*x[28] + 0*x[29] + 0*x[30] + x[31] + x[32] + x[33] + 0*x[34] + 0*x[35] + x[36] + x[37] + 0*x[38] + x[39] + x[40] + 0*x[41] + x[42] + x[43] + 0*x[44] + 0*x[45] + 0*x[46] + 0*x[47] + 0*x[48] + 0*x[49] + 0*x[50] + 0*x[51] + x[52] + x[53] + 0*x[54] + x[55] + x[56] + 0*x[57] + 0*x[58] + x[59] + x[60] + 0*x[61] + 0*x[62] + 0*x[63] + x[64] + 0*x[65] + 0*x[66] + 0*x[67] + 0*x[68] + x[69] + 0*x[70] + 0*x[71] + x[72] + x[73] + x[74] + x[75] + 0*x[76] + x[77] + 0*x[78] + 0*x[79] + 0*x[80] + 0*x[81] + 0*x[82] + x[83] + 0*x[84] + 0*x[85] + 0*x[86] + 0*x[87] + 0*x[88] + 0*x[89] + 0*x[90] + 0*x[91] + 0*x[92] + 0*x[93] + x[94] + 0*x[95] + 0*x[96] + 0*x[97] + x[98] + 0*x[99] + 0*x[100] + x[101] + 0*x[102] + x[103] + 0*x[104] + 0*x[105] + x[106] + x[107] + 0*x[108] + 0*x[109] + 0*x[110] + x[111] + 0*x[112] + x[113] + 0*x[114] + 0*x[115] + 0*x[116] + x[117] + 0*x[118] + 0*x[119] + 0*x[120] + 0*x[121] + x[122] + 0*x[123] + 0*x[124] + 0*x[125] + 0*x[126] + x[127] + x[128] + 0*x[129] + 0*x[130] + 0*x[131] + 0*x[132] + 0*x[133] + x[134] + 0*x[135] + 0*x[136] + x[137] + 0*x[138] + x[139] + x[140] + 0*x[141] + x[142] + 0*x[143] + x[144] + x[145] + 0*x[146] + 0*x[147] + 0*x[148] + x[149] + x[150] + 0*x[151] + x[152] + 0*x[153] + 0*x[154] + 0*x[155] + x[156] + x[157] + x[158] + x[159] + 0*x[160] + x[161] + 0*x[162] + 0*x[163] + 0*x[164] + 0*x[165] + x[166] + 0*x[167] + 0*x[168] + 0*x[169] + 0*x[170] + 0*x[171] + 0*x[172] + x[173] + 0*x[174] + x[175] + x[176] + 0*x[177] + x[178] + 0*x[179] + 0*x[180] + 0*x[181] + 0*x[182] + 0*x[183] + x[184] + 0*x[185] + x[186] + 0*x[187] + 0*x[188] + 0*x[189] + 0*x[190] + 0*x[191] + x[192] + x[193] + 0*x[194] + x[195] + x[196] + x[197] + x[198] + 0*x[199] + 0*x[200] + x[201] + x[202] + x[203] + 0*x[204] + x[205] + 0*x[206] + 0*x[207] + x[208] + 0*x[209] + x[210] + x[211] + 0*x[212] + 0*x[213] + x[214] + 0*x[215] + x[216] + 0*x[217] + 0*x[218] + x[219] + 0*x[220] + x[221] + 0*x[222] + 0*x[223] + 0*x[224] + x[225] + x[226] + x[227] + x[228] + x[229] + x[230] + 0*x[231] + 0*x[232] + 0*x[233] + x[234] + 0*x[235] + x[236] + x[237] + 0*x[238] + x[239] + x[240] + 0*x[241] + 0*x[242] + 0*x[243] + x[244] + 0*x[245] + 0*x[246] + x[247] + 0*x[248] + 0*x[249] + x[250] + 0*x[251] + x[252] + 0*x[253] + 0*x[254] + 0*x[255] + x[256] + 0*x[257] + 0*x[258] + 0*x[259] + 0*x[260] + 0*x[261] + x[262] + x[263] + 0*x[264] + 0*x[265] + x[266] + x[267] + x[268] + 0*x[269] + 0*x[270] + x[271] + x[272] + 0*x[273] + 0*x[274] + 0*x[275] + x[276] + 0*x[277] + 0*x[278] + x[279] + x[280] + 0*x[281] + 0*x[282] + x[283] + 0*x[284] + 0*x[285] + x[286] + x[287] + 0*x[288] + 0*x[289] + 0*x[290] + 0*x[291] + 0*x[292] + x[293] + 0*x[294] + 0*x[295] + 0*x[296] + 0*x[297] + 0*x[298] + x[299] + 0*x[300] + 0*x[301] + x[302] + 0*x[303] + 0*x[304] + x[305] + 0*x[306] + 0*x[307] + x[308] + x[309] + 0*x[310] + x[311] + 0*x[312] + 0*x[313] + x[314] + 0*x[315] + 0*x[316] + x[317] + 0*x[318] + 0*x[319] + x[320] + 0*x[321] + 0*x[322] + 0*x[323] + 0*x[324] + 0*x[325] + x[326] + 0*x[327] + 0*x[328] + 0*x[329] + 0*x[330] + 0*x[331] + 0*x[332] + 0*x[333] + 0*x[334] + x[335] + x[336] + 0*x[337] + 0*x[338] + 0*x[339] + 0*x[340] + x[341] + 0*x[342] + 0*x[343] + x[344] + 0*x[345] + x[346] + 0*x[347] + 0*x[348] + 0*x[349] + 0*x[350] + 0*x[351] + x[352] + 0*x[353] + 0*x[354] + 0*x[355] + 0*x[356] + 0*x[357] + 0*x[358] + 0*x[359] + 0*x[360] + x[361] + x[362] + 0*x[363] + x[364] + 0*x[365] + 0*x[366] + 0*x[367] + x[368] + 0*x[369] + 0*x[370] + 0*x[371] + 0*x[372] + 0*x[373] + x[374] + 0*x[375] + 0*x[376] + 0*x[377] + 0*x[378] + x[379] + x[380] + x[381] + x[382] + 0*x[383] + 0*x[384] + 0*x[385] + 0*x[386] + x[387] + 0*x[388] + 0*x[389] + 0*x[390] + x[391] : 4.0 : True
num_positionConstraint : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 9.0 : x[0] + x[1] + x[2] + x[3] + x[4] + x[5] + x[6] + x[7] + x[8] + x[9] + x[10] + x[11] + x[12] + x[13] + x[14] + x[15] + x[16] + x[17] + x[18] + x[19] + x[20] + x[21] + x[22] + x[23] + x[24] + x[25] + x[26] + x[27] + x[28] + x[29] + x[30] + x[31] + x[32] + x[33] + x[34] + x[35] + x[36] + x[37] + x[38] + x[39] + x[40] + x[41] + x[42] + x[43] + x[44] + x[45] + x[46] + x[47] + x[48] + x[49] + x[50] + x[51] + x[52] + x[53] + x[54] + x[55] + x[56] + x[57] + x[58] + x[59] + x[60] + x[61] + x[62] + x[63] + x[64] + x[65] + x[66] + x[67] + x[68] + x[69] + x[70] + x[71] + x[72] + x[73] + x[74] + x[75] + x[76] + x[77] + x[78] + x[79] + x[80] + x[81] + x[82] + x[83] + x[84] + x[85] + x[86] + x[87] + x[88] + x[89] + x[90] + x[91] + x[92] + x[93] + x[94] + x[95] + x[96] + x[97] + x[98] + x[99] + x[100] + x[101] + x[102] + x[103] + x[104] + x[105] + x[106] + x[107] + x[108] + x[109] + x[110] + x[111] + x[112] + x[113] + x[114] + x[115] + x[116] + x[117] + x[118] + x[119] + x[120] + x[121] + x[122] + x[123] + x[124] + x[125] + x[126] + x[127] + x[128] + x[129] + x[130] + x[131] + x[132] + x[133] + x[134] + x[135] + x[136] + x[137] + x[138] + x[139] + x[140] + x[141] + x[142] + x[143] + x[144] + x[145] + x[146] + x[147] + x[148] + x[149] + x[150] + x[151] + x[152] + x[153] + x[154] + x[155] + x[156] + x[157] + x[158] + x[159] + x[160] + x[161] + x[162] + x[163] + x[164] + x[165] + x[166] + x[167] + x[168] + x[169] + x[170] + x[171] + x[172] + x[173] + x[174] + x[175] + x[176] + x[177] + x[178] + x[179] + x[180] + x[181] + x[182] + x[183] + x[184] + x[185] + x[186] + x[187] + x[188] + x[189] + x[190] + x[191] + x[192] + x[193] + x[194] + x[195] + x[196] + x[197] + x[198] + x[199] + x[200] + x[201] + x[202] + x[203] + x[204] + x[205] + x[206] + x[207] + x[208] + x[209] + x[210] + x[211] + x[212] + x[213] + x[214] + x[215] + x[216] + x[217] + x[218] + x[219] + x[220] + x[221] + x[222] + x[223] + x[224] + x[225] + x[226] + x[227] + x[228] + x[229] + x[230] + x[231] + x[232] + x[233] + x[234] + x[235] + x[236] + x[237] + x[238] + x[239] + x[240] + x[241] + x[242] + x[243] + x[244] + x[245] + x[246] + x[247] + x[248] + x[249] + x[250] + x[251] + x[252] + x[253] + x[254] + x[255] + x[256] + x[257] + x[258] + x[259] + x[260] + x[261] + x[262] + x[263] + x[264] + x[265] + x[266] + x[267] + x[268] + x[269] + x[270] + x[271] + x[272] + x[273] + x[274] + x[275] + x[276] + x[277] + x[278] + x[279] + x[280] + x[281] + x[282] + x[283] + x[284] + x[285] + x[286] + x[287] + x[288] + x[289] + x[290] + x[291] + x[292] + x[293] + x[294] + x[295] + x[296] + x[297] + x[298] + x[299] + x[300] + x[301] + x[302] + x[303] + x[304] + x[305] + x[306] + x[307] + x[308] + x[309] + x[310] + x[311] + x[312] + x[313] + x[314] + x[315] + x[316] + x[317] + x[318] + x[319] + x[320] + x[321] + x[322] + x[323] + x[324] + x[325] + x[326] + x[327] + x[328] + x[329] + x[330] + x[331] + x[332] + x[333] + x[334] + x[335] + x[336] + x[337] + x[338] + x[339] + x[340] + x[341] + x[342] + x[343] + x[344] + x[345] + x[346] + x[347] + x[348] + x[349] + x[350] + x[351] + x[352] + x[353] + x[354] + x[355] + x[356] + x[357] + x[358] + x[359] + x[360] + x[361] + x[362] + x[363] + x[364] + x[365] + x[366] + x[367] + x[368] + x[369] + x[370] + x[371] + x[372] + x[373] + x[374] + x[375] + x[376] + x[377] + x[378] + x[379] + x[380] + x[381] + x[382] + x[383] + x[384] + x[385] + x[386] + x[387] + x[388] + x[389] + x[390] + x[391] : 9.0 : True
10 Declarations: x Objective BudgetConstraint num_positionConstraint QBConstraint RBConstraint WRConstraint TEConstraint DEFConstraint RSTConstraint
#solve the model
opt = SolverFactory('cbc')
opt.options['seconds'] = 5 #specifies the time limit (in seconds)
#####QUESTION C SOLUTION########### change the ratioGap below to zero:
opt.options['ratioGap'] = 0 #specifies the optimality gap tolerance (.01 means alg can stop if guarenteed within <1% of optimal obj)
results = opt.solve(model, tee=True)
Welcome to the CBC MILP Solver
Version: 2.10.10
Build Date: Jun 7 2023
command line - /content/bin/cbc -seconds 5 -ratioGap 0 -printingOptions all -import /tmp/tmphsoq417g.pyomo.lp -stat=1 -solve -solu /tmp/tmphsoq417g.pyomo.soln (default strategy 1)
seconds was changed from 1e+100 to 5
ratioGap was changed from 0 to 0
Option for printingOptions changed from normal to all
CoinLpIO::readLp(): Maximization problem reformulated as minimization
Coin0009I Switching back to maximization to get correct duals etc
Presolve 8 (0) rows, 392 (0) columns and 1335 (-74) elements
Statistics for presolved model
Original problem has 392 integers (392 of which binary)
==== 135 zero objective 235 different
==== absolute objective values 235 different
==== for integers 135 zero objective 235 different
==== for integers absolute objective values 235 different
===== end objective counts
Problem has 8 rows, 392 columns (257 with objective) and 1335 elements
Column breakdown:
0 of type 0.0->inf, 0 of type 0.0->up, 0 of type lo->inf,
0 of type lo->up, 0 of type free, 0 of type fixed,
0 of type -inf->0.0, 0 of type -inf->up, 392 of type 0.0->1.0
Row breakdown:
0 of type E 0.0, 2 of type E 1.0, 0 of type E -1.0,
1 of type E other, 0 of type G 0.0, 0 of type G 1.0,
1 of type G other, 0 of type L 0.0, 0 of type L 1.0,
4 of type L other, 0 of type Range 0.0->1.0, 0 of type Range other,
0 of type Free
Continuous objective value is 128.03 - 0.00 seconds
Cgl0003I 0 fixed, 2 tightened bounds, 0 strengthened rows, 0 substitutions
Cgl0004I processed model has 8 rows, 274 columns (274 integer (271 of which binary)) and 1055 elements
Cutoff increment increased from 1e-05 to 0.00999
Cbc0038I Initial state - 2 integers unsatisfied sum - 0.75
Cbc0038I Pass 1: suminf. 0.08824 (2) obj. 127.704 iterations 5
Cbc0038I Pass 2: suminf. 0.00000 (0) obj. 105.7 iterations 6
Cbc0038I Solution found of 105.7
Cbc0038I Cleaned solution of 105.7
Cbc0038I Before mini branch and bound, 270 integers at bound fixed and 0 continuous
Cbc0038I Full problem 8 rows 274 columns, reduced to 3 rows 4 columns
Cbc0038I Mini branch and bound improved solution from 105.7 to 126.88 (0.02 seconds)
Cbc0038I Round again with cutoff of 127.004
Cbc0038I Reduced cost fixing fixed 243 variables on major pass 2
Cbc0038I Pass 3: suminf. 0.09375 (2) obj. 127.966 iterations 2
Cbc0038I Pass 4: suminf. 0.21343 (2) obj. 127.004 iterations 4
Cbc0038I Pass 5: suminf. 0.86036 (3) obj. 127.004 iterations 10
Cbc0038I Solution found of 127.21
Cbc0038I Cleaned solution of 127.21
Cbc0038I Before mini branch and bound, 268 integers at bound fixed and 0 continuous
Cbc0038I Full problem 8 rows 274 columns, reduced to 3 rows 6 columns
Cbc0038I Mini branch and bound did not improve solution (0.02 seconds)
Cbc0038I Round again with cutoff of 127.382
Cbc0038I Reduced cost fixing fixed 253 variables on major pass 3
Cbc0038I Pass 6: suminf. 0.09375 (2) obj. 127.966 iterations 0
Cbc0038I Pass 7: suminf. 0.16642 (2) obj. 127.382 iterations 3
Cbc0038I Pass 8: suminf. 1.00000 (3) obj. 127.382 iterations 12
Cbc0038I Pass 9: suminf. 0.22346 (2) obj. 127.382 iterations 6
Cbc0038I Pass 10: suminf. 0.17590 (2) obj. 127.382 iterations 3
Cbc0038I Pass 11: suminf. 1.00000 (3) obj. 127.382 iterations 7
Cbc0038I Pass 12: suminf. 0.96384 (3) obj. 127.382 iterations 3
Cbc0038I Pass 13: suminf. 0.96384 (3) obj. 127.382 iterations 2
Cbc0038I Pass 14: suminf. 0.30335 (2) obj. 127.382 iterations 5
Cbc0038I Pass 15: suminf. 0.30335 (2) obj. 127.382 iterations 0
Cbc0038I Pass 16: suminf. 1.00000 (3) obj. 127.382 iterations 6
Cbc0038I Pass 17: suminf. 0.96384 (3) obj. 127.382 iterations 3
Cbc0038I Pass 18: suminf. 0.96384 (3) obj. 127.382 iterations 2
Cbc0038I Pass 19: suminf. 0.30335 (2) obj. 127.382 iterations 5
Cbc0038I Pass 20: suminf. 0.30335 (2) obj. 127.382 iterations 0
Cbc0038I Pass 21: suminf. 1.00000 (3) obj. 127.382 iterations 6
Cbc0038I Pass 22: suminf. 0.96384 (3) obj. 127.382 iterations 3
Cbc0038I Pass 23: suminf. 0.96384 (3) obj. 127.382 iterations 2
Cbc0038I Pass 24: suminf. 0.30335 (2) obj. 127.382 iterations 5
Cbc0038I Pass 25: suminf. 0.30335 (2) obj. 127.382 iterations 0
Cbc0038I Pass 26: suminf. 1.00000 (3) obj. 127.382 iterations 6
Cbc0038I Pass 27: suminf. 0.96384 (3) obj. 127.382 iterations 3
Cbc0038I Pass 28: suminf. 0.96384 (3) obj. 127.382 iterations 2
Cbc0038I Pass 29: suminf. 0.30335 (2) obj. 127.382 iterations 5
Cbc0038I Pass 30: suminf. 0.30335 (2) obj. 127.382 iterations 0
Cbc0038I Pass 31: suminf. 1.00000 (3) obj. 127.382 iterations 6
Cbc0038I Pass 32: suminf. 0.96384 (3) obj. 127.382 iterations 3
Cbc0038I Pass 33: suminf. 0.96384 (3) obj. 127.382 iterations 2
Cbc0038I Pass 34: suminf. 0.30335 (2) obj. 127.382 iterations 5
Cbc0038I Pass 35: suminf. 0.30335 (2) obj. 127.382 iterations 0
Cbc0038I No solution found this major pass
Cbc0038I Before mini branch and bound, 267 integers at bound fixed and 0 continuous
Cbc0038I Full problem 8 rows 274 columns, reduced to 3 rows 6 columns
Cbc0038I Mini branch and bound improved solution from 127.21 to 127.36 (0.04 seconds)
Cbc0038I Round again with cutoff of 127.576
Cbc0038I Reduced cost fixing fixed 257 variables on major pass 4
Cbc0038I Pass 35: suminf. 0.09375 (2) obj. 127.966 iterations 0
Cbc0038I Pass 36: suminf. 0.14224 (2) obj. 127.576 iterations 3
Cbc0038I Pass 37: suminf. 0.39199 (4) obj. 127.576 iterations 7
Cbc0038I Pass 38: suminf. 0.38490 (4) obj. 127.576 iterations 1
Cbc0038I Pass 39: suminf. 1.00000 (3) obj. 127.576 iterations 7
Cbc0038I Pass 40: suminf. 1.00000 (3) obj. 127.576 iterations 2
Cbc0038I Pass 41: suminf. 0.75695 (2) obj. 127.576 iterations 7
Cbc0038I Pass 42: suminf. 0.29634 (2) obj. 127.576 iterations 1
Cbc0038I Pass 43: suminf. 0.95576 (3) obj. 127.576 iterations 5
Cbc0038I Pass 44: suminf. 0.29634 (2) obj. 127.576 iterations 3
Cbc0038I Pass 45: suminf. 0.64783 (2) obj. 127.576 iterations 3
Cbc0038I Pass 46: suminf. 0.39421 (2) obj. 127.576 iterations 1
Cbc0038I Pass 47: suminf. 0.79723 (3) obj. 127.576 iterations 5
Cbc0038I Pass 48: suminf. 0.98581 (3) obj. 127.576 iterations 2
Cbc0038I Pass 49: suminf. 1.00000 (3) obj. 127.576 iterations 4
Cbc0038I Pass 50: suminf. 0.88787 (3) obj. 127.576 iterations 4
Cbc0038I Pass 51: suminf. 0.16442 (2) obj. 127.576 iterations 3
Cbc0038I Pass 52: suminf. 0.88787 (3) obj. 127.576 iterations 5
Cbc0038I Pass 53: suminf. 0.39199 (4) obj. 127.576 iterations 9
Cbc0038I Pass 54: suminf. 0.38490 (4) obj. 127.576 iterations 1
Cbc0038I Pass 55: suminf. 1.00000 (3) obj. 127.576 iterations 7
Cbc0038I Pass 56: suminf. 1.00000 (3) obj. 127.576 iterations 2
Cbc0038I Pass 57: suminf. 0.75695 (2) obj. 127.576 iterations 7
Cbc0038I Pass 58: suminf. 0.29634 (2) obj. 127.576 iterations 1
Cbc0038I Pass 59: suminf. 0.95576 (3) obj. 127.576 iterations 5
Cbc0038I Pass 60: suminf. 0.29634 (2) obj. 127.576 iterations 3
Cbc0038I Pass 61: suminf. 0.29398 (2) obj. 127.576 iterations 5
Cbc0038I Pass 62: suminf. 0.28125 (2) obj. 127.679 iterations 1
Cbc0038I Pass 63: suminf. 0.29398 (2) obj. 127.576 iterations 3
Cbc0038I Pass 64: suminf. 0.29398 (2) obj. 127.576 iterations 2
Cbc0038I No solution found this major pass
Cbc0038I Before mini branch and bound, 262 integers at bound fixed and 0 continuous
Cbc0038I Full problem 8 rows 274 columns, reduced to 6 rows 12 columns
Cbc0038I Mini branch and bound improved solution from 127.36 to 127.56 (0.05 seconds)
Cbc0038I Round again with cutoff of 127.712
Cbc0038I Reduced cost fixing fixed 262 variables on major pass 5
Cbc0038I Pass 64: suminf. 0.09375 (2) obj. 127.966 iterations 0
Cbc0038I Pass 65: suminf. 0.12531 (2) obj. 127.712 iterations 3
Cbc0038I Pass 66: suminf. 0.87962 (3) obj. 127.712 iterations 6
Cbc0038I Pass 67: suminf. 0.38845 (3) obj. 127.712 iterations 3
Cbc0038I Pass 68: suminf. 0.38845 (3) obj. 127.712 iterations 0
Cbc0038I Pass 69: suminf. 0.69393 (2) obj. 127.712 iterations 3
Cbc0038I Pass 70: suminf. 1.68765 (4) obj. 127.712 iterations 1
Cbc0038I Pass 71: suminf. 1.00000 (3) obj. 127.712 iterations 3
Cbc0038I Pass 72: suminf. 1.00000 (3) obj. 127.712 iterations 2
Cbc0038I Pass 73: suminf. 0.60299 (2) obj. 127.712 iterations 6
Cbc0038I Pass 74: suminf. 0.15625 (2) obj. 127.774 iterations 4
Cbc0038I Pass 75: suminf. 0.16387 (2) obj. 127.712 iterations 2
Cbc0038I Pass 76: suminf. 0.30156 (3) obj. 127.712 iterations 4
Cbc0038I Pass 77: suminf. 1.03304 (4) obj. 127.712 iterations 4
Cbc0038I Pass 78: suminf. 0.66337 (4) obj. 127.712 iterations 4
Cbc0038I Pass 79: suminf. 1.03304 (4) obj. 127.712 iterations 2
Cbc0038I Pass 80: suminf. 0.16573 (2) obj. 127.712 iterations 7
Cbc0038I Pass 81: suminf. 0.08814 (2) obj. 127.712 iterations 3
Cbc0038I Pass 82: suminf. 0.41521 (3) obj. 127.712 iterations 6
Cbc0038I Pass 83: suminf. 0.42093 (4) obj. 127.712 iterations 3
Cbc0038I Pass 84: suminf. 0.16573 (2) obj. 127.712 iterations 4
Cbc0038I Pass 85: suminf. 0.91587 (4) obj. 127.712 iterations 7
Cbc0038I Pass 86: suminf. 0.62843 (3) obj. 127.712 iterations 1
Cbc0038I Pass 87: suminf. 0.75000 (2) obj. 127.88 iterations 4
Cbc0038I Pass 88: suminf. 0.30201 (2) obj. 127.712 iterations 4
Cbc0038I Pass 89: suminf. 0.86650 (3) obj. 127.712 iterations 5
Cbc0038I Pass 90: suminf. 0.86650 (3) obj. 127.712 iterations 0
Cbc0038I Pass 91: suminf. 1.00000 (3) obj. 127.712 iterations 1
Cbc0038I Pass 92: suminf. 0.55556 (2) obj. 127.816 iterations 4
Cbc0038I Pass 93: suminf. 0.15625 (2) obj. 127.774 iterations 2
Cbc0038I No solution found this major pass
Cbc0038I Before mini branch and bound, 264 integers at bound fixed and 0 continuous
Cbc0038I Full problem 8 rows 274 columns, reduced to 3 rows 9 columns
Cbc0038I Mini branch and bound did not improve solution (0.07 seconds)
Cbc0038I After 0.07 seconds - Feasibility pump exiting with objective of 127.56 - took 0.06 seconds
Cbc0012I Integer solution of 127.56 found by feasibility pump after 0 iterations and 0 nodes (0.07 seconds)
Cbc0038I Full problem 8 rows 274 columns, reduced to 2 rows 4 columns
Cbc0031I 7 added rows had average density of 8
Cbc0013I At root node, 7 cuts changed objective from 128.03 to 127.60498 in 11 passes
Cbc0014I Cut generator 0 (Probing) - 2 row cuts average 7.0 elements, 1 column cuts (1 active) in 0.001 seconds - new frequency is 1
Cbc0014I Cut generator 1 (Gomory) - 0 row cuts average 0.0 elements, 0 column cuts (0 active) in 0.002 seconds - new frequency is -100
Cbc0014I Cut generator 2 (Knapsack) - 11 row cuts average 12.8 elements, 0 column cuts (0 active) in 0.004 seconds - new frequency is 1
Cbc0014I Cut generator 3 (Clique) - 0 row cuts average 0.0 elements, 0 column cuts (0 active) in 0.000 seconds - new frequency is -100
Cbc0014I Cut generator 4 (MixedIntegerRounding2) - 2 row cuts average 8.5 elements, 0 column cuts (0 active) in 0.002 seconds - new frequency is -100
Cbc0014I Cut generator 5 (FlowCover) - 0 row cuts average 0.0 elements, 0 column cuts (0 active) in 0.000 seconds - new frequency is -100
Cbc0014I Cut generator 6 (TwoMirCuts) - 44 row cuts average 9.8 elements, 0 column cuts (0 active) in 0.006 seconds - new frequency is -100
Cbc0014I Cut generator 7 (ZeroHalf) - 8 row cuts average 274.0 elements, 0 column cuts (0 active) in 0.005 seconds - new frequency is -100
Cbc0001I Search completed - best objective 127.56, took 49 iterations and 0 nodes (0.11 seconds)
Cbc0032I Strong branching done 16 times (51 iterations), fathomed 1 nodes and fixed 0 variables
Cbc0035I Maximum depth 0, 257 variables fixed on reduced cost
Cuts at root node changed objective from 128.03 to 127.115
Probing was tried 11 times and created 3 cuts of which 0 were active after adding rounds of cuts (0.001 seconds)
Gomory was tried 11 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.002 seconds)
Knapsack was tried 11 times and created 11 cuts of which 0 were active after adding rounds of cuts (0.004 seconds)
Clique was tried 11 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
MixedIntegerRounding2 was tried 11 times and created 2 cuts of which 0 were active after adding rounds of cuts (0.002 seconds)
FlowCover was tried 11 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
TwoMirCuts was tried 11 times and created 44 cuts of which 0 were active after adding rounds of cuts (0.006 seconds)
ZeroHalf was tried 11 times and created 8 cuts of which 0 were active after adding rounds of cuts (0.005 seconds)
Result - Optimal solution found
Objective value: 127.56000000
Enumerated nodes: 0
Total iterations: 49
Time (CPU seconds): 0.11
Time (Wallclock seconds): 0.39
Total time (CPU seconds): 0.12 (Wallclock seconds): 0.41
This is the optimized lineup with the highest projected fantasy points based on a budget of $50,000 and a roster percentage greater than or equal to 6 percent.
#print out solution
pos = []
player = []
points = []
print("Choose theses players: ")
for i in range(n):
if model.x[i]() == 1:
print(df.loc[i]['POS'])
pos.append(df.loc[i]['POS'])
print(df.loc[i]['PLAYER'])
player.append(df.loc[i]['PLAYER'])
print(df.loc[i]['FPTS'])
points.append(df.loc[i]['FPTS'])
print("Total Projected Points:", model.Objective())
print("Total Budget:", model.BudgetConstraint())
print("Average Roster Percet", model.RSTConstraint())
Choose theses players:
RB
Ezekiel Elliott
15.19
RB
Christian McCaffrey
23.02
RB
Antonio Gibson
14.64
WR
Garrett Wilson
14.06
WR
Terry McLaurin
13.36
D
Carolina Panthers
6.89
TE
Chigoziem Okonkwo
6.94
QB
Josh Allen
23.46
WR
Rashid Shaheed
10.0
Total Projected Points: 127.56
Total Budget: 49900.0
Average Roster Percet 15.704444444444444
I have created an excel output to load the lineup into a Daily Fantasy Sports site.
excel_output = pd.DataFrame({'Position': pos, 'Player': player, 'Projected Points': points})
excel_output
| Position | Player | Projected Points | |
|---|---|---|---|
| 0 | RB | Ezekiel Elliott | 15.19 |
| 1 | RB | Christian McCaffrey | 23.02 |
| 2 | RB | Antonio Gibson | 14.64 |
| 3 | WR | Garrett Wilson | 14.06 |
| 4 | WR | Terry McLaurin | 13.36 |
| 5 | D | Carolina Panthers | 6.89 |
| 6 | TE | Chigoziem Okonkwo | 6.94 |
| 7 | QB | Josh Allen | 23.46 |
| 8 | WR | Rashid Shaheed | 10.00 |
excel_output.to_excel('output.xlsx', sheet_name='Lineup 1', index=False)
